Question

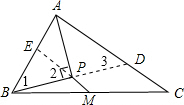
如图，在△ABC中，M是BC边的中点，AP平分∠A，BP⊥AP于点P、若AB=12，AC=22，则MP的长为______．

Answer 1

延长BP与AC相交于D，延长MP与AB相交于E
因为∠BAP=∠DAP，AP⊥BD，AP=AP
所以△ABP≌△APD
于是BP=PD
又∵M是BC边的中点
故PM∥AC
所以∠2=∠3
又因为∠1=∠3
所以∠1=∠2，EP=AE=

1

2

AB=

1

2

×12=6
AD=2EP=2×6=12
DC=22-12=10
PM=

1

2

DC=

1

2

×10=5
故MP的长为5．
故答案为5．