题目内容
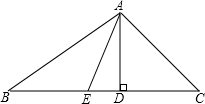
如图所示，△ABC中，∠B：∠C=3：4，FD⊥BC，DE⊥AB，且∠AFD=146°，求∠EDF的度数．
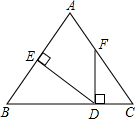
∵∠AFD=146°，FD⊥BC，
∴∠C=∠AFD-∠FDC=146°-90°=56°，
∵∠B：∠C=3：4，
∴∠B=56°×
=42°，
∵DE⊥AB，
∴∠BED=90°，
∴∠BDE=90°-42°=48°，
∵∠BDE+∠EDF=90°，
∴∠EDF=90°-∠BDE=90°-48°=42°．
∴∠C=∠AFD-∠FDC=146°-90°=56°，
∵∠B：∠C=3：4，
∴∠B=56°×
| 3 |
| 4 |
∵DE⊥AB，
∴∠BED=90°，
∴∠BDE=90°-42°=48°，
∵∠BDE+∠EDF=90°，
∴∠EDF=90°-∠BDE=90°-48°=42°．
练习册系列答案
名校课堂系列答案
相关题目
