题目内容
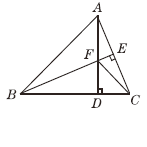
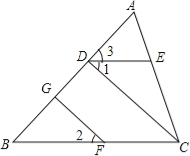
【题目】∠1=∠2,∠3=∠B,FG⊥AB于G,猜想CD与AB的关系,并证明你的猜想.
【答案】垂直,证明见解析
【解析】试题分析:根据∠3=∠B得出ED∥BC,根据FG⊥AB得出∠AGF=90°,根据外角的性质得出∠AGF=∠B+∠2,结合∠ADC=∠1+∠3,∠1=∠2,∠3=∠B从而得出∠ADC=∠AGF=90°,从而得到垂直.
试题解析:猜想CD⊥AB.
理由如下: ∵∠3=∠B(已知),∴ED∥BC(同位角相等,两直线平行).
∵FG⊥AB(已知),∴∠AGF=90°(垂直定义).
∵∠AGF是△BFG的一个外角, ∴∠AGF=∠B+∠2(三角形的一个外角等于和它不相邻的两个内角的和).
∵∠ADC=∠1+∠3,而∠1=∠2,∠3=∠B, ∴∠ADC=∠AGF=90°(等量代换).
∴CD⊥AB(垂直定义).

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目