题目内容
如图,以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,C为切点.若两圆的半径分别为3cm和5cm,则AB的长为_____cm.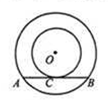

8
连接OC、OA;由切线的性质知:OC⊥AB;在Rt△OAC中,可由勾股定理求得AC的长;根据垂径定理知:AB=2AC,由此得解.
解:连接OC、OA,
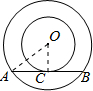
∵AB切⊙O于C,
∴OC⊥AB,
∴AB=2AC;
∵在Rt△OAC中,OA=5cm,OC=3cm,
∴AC=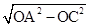 =4cm,
=4cm,
∴AB=2AC=8cm.
解:连接OC、OA,

∵AB切⊙O于C,
∴OC⊥AB,
∴AB=2AC;
∵在Rt△OAC中,OA=5cm,OC=3cm,
∴AC=
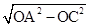 =4cm,
=4cm,∴AB=2AC=8cm.

练习册系列答案
相关题目
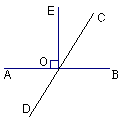
 ∠BOD,
∠BOD,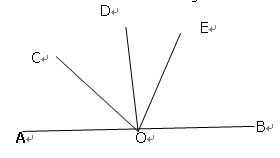
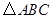 中,∠C=90°,BC=3cm,AC=4cm,则
中,∠C=90°,BC=3cm,AC=4cm,则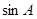 的值为( ).
的值为( ).



 的补角是
的补角是 ,则
,则 度
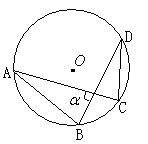
度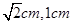 ,则弦AC、BD所夹的锐角
,则弦AC、BD所夹的锐角 = .
= .

 ,
, 于
于 ,
, 交
交 于
于 ,已知
,已知 ,则
,则 是
是



