题目内容
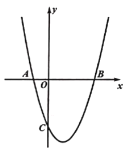
【题目】抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,该抛物线与
,该抛物线与![]() 轴的两个交点分别为
轴的两个交点分别为![]() 和
和![]() ,与
,与![]() 轴的交点为
轴的交点为![]() ,其中
,其中![]() .
.
(1)写出点![]() 的坐标________;
的坐标________;
(2)若抛物线上存在一点![]() ,使得
,使得![]() 的面积是
的面积是![]() 的面积的
的面积的![]() 倍,求点
倍,求点![]() 的坐标;
的坐标;
(3)点![]() 是线段
是线段![]() 上一点,过点
上一点,过点![]() 作
作![]() 轴的垂线交抛物线于点
轴的垂线交抛物线于点![]() ,求线段
,求线段![]() 长度的最大值.
长度的最大值.
【答案】(1)![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() 或
或![]() ;(3)MD长度的最大值为
;(3)MD长度的最大值为![]() .
.
【解析】
(1)抛物线的对称轴为x=1,点A坐标为(-1,0),则点B(3,0),即可求解;
(2)由S△POC=2S△BOC,则x=±2OB=6,即可求解;
(3)设:点M坐标为(x,x-3),则点D坐标为(x,x2-2x-3),则MD=x-3-x2+2x+3,即可求解.
解:(1)抛物线的对称轴为![]() ,点
,点![]() 坐标为
坐标为![]() ,则点
,则点![]() ,
,
故:答案为![]() ;
;
(2)二次函数表达式为:![]() ,
,
即:![]() ,解得:
,解得:![]() ,
,
故抛物线的表达式为:![]() ,
,
所以![]()
由题意得:![]() ,
,
设P(x, ![]() )
)
则![]()
所以![]() 则
则![]() ,
,
所以当![]() 时,
时,![]() =-21,当
=-21,当![]() 时,
时,![]() =45
=45
故点![]() 的坐标为
的坐标为![]() 或
或![]() ;
;
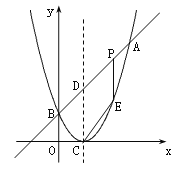
(3)如图所示,
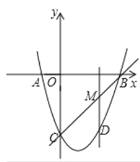
将点![]() 坐标代入一次函数
坐标代入一次函数![]() 得表达式得
得表达式得
![]() ,解得:
,解得:![]() ,
,
故直线![]() 的表达式为:
的表达式为:
![]() ,
,
设:点![]() 坐标为
坐标为![]() ,则点
,则点![]() 坐标为
坐标为![]() ,
,
则![]() ,
,
故MN长度的最大值为![]() .
.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
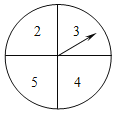
【题目】如图所示,有一个可以自由转动的转盘,其盘面分为4等份,在每一等份分别标有对应的数字2,3,4,5.小明打算自由转动转盘10次,现已经转动了8次,每一次停止后,小明将指针所指数字记录如下:
次数 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | 第7次 | 第8次 | 第9次 | 第10次 |
数字 | 3 | 5 | 2 | 3 | 3 | 4 | 3 | 5 |
(1)求前8次的指针所指数字的平均数.
(2)小明继续自由转动转盘2次,判断是否可能发生“这10次的指针所指数字的平均数不小于3.3,且不大于3.5”的结果?若有可能,计算发生此结果的概率,并写出计算过程;若不可能,说明理由.(指针指向盘面等分线时为无效转次.)