题目内容
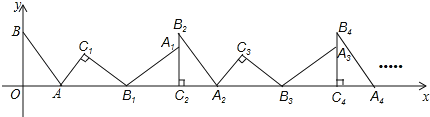
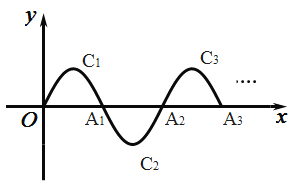
【题目】如图所示，一段抛物线：
，记为
，它与
轴交于点
，
；
将绕点旋转
得
，交轴于点
；
将绕点旋转得
，交轴于点
；
如此进行下去，直到
.若
在第13段抛物线上，则
______.
【答案】2
【解析】
求出抛物线C1与x轴的交点坐标，观察图形可知第奇数号抛物线都在x轴上方，然后求出到抛物线C13平移的距离，再根据向右平移横坐标加表示出抛物线C13的解析式，然后把点P的坐标代入计算即可得解．
解：令y=0，则-x（x-3）=0，
解得x1=0，x2=3，
∴A1（3，0），
由图可知，抛物线C13在x轴上方，
相当于抛物线C1向右平移6×6=36个单位得到，
∴抛物线C13的解析式为y=-（x-36）（x-36-3）=-（x-36）（x-39），
∵P（37，m）在第13段抛物线C13上，
∴m=-（37-36）（37-39）=2．
故答案为：2
每课必练系列答案
巧学巧练系列答案
【题目】甲、乙两名队员的10次射击训练，成绩分别被制成下列两个统计图.
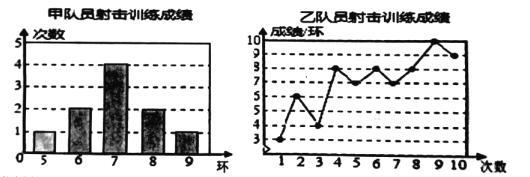
并整理分析数据如下表：
平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
甲 |
| 7 | 7 | 1.2 |
乙 | 7 |
| 8 |
|
（1）求
，
，
的值；
（2）分别运用表中的四个统计量，简要分析这两名队员的射击训练成绩.若选派其中一名参赛，你认为应选哪名队员？
【题目】某网上书店以每本24元的价格购进了600本某种畅销书籍（定价每本45元），第一个月以每本36元销售，卖出了200本；第二个月书店为了增加销售量，决定在第一个月价格的基础上降价销售，根据市场调查，每本书每降低1元，可多售出20本，但最低售价应高于购进的价格.第二个月结束后，书店将剩余的书籍捐赠给某希望学校，设第二个月每本降低
元.
（1）填表：（列式，不需要化简）
时间 | 第一个月 | 第二个月 |
每本售价（元） | 36 | |
销售量（本） | 200 |
（2）如果该书店希望通过销售这批书籍获利2400元，那么第二个月每本书的售价应是多少元？
