Question

【题目】如图，AD为等边△ABC的高，E、F分别为线段AD、AC上的动点，且AE＝CF，当BF＋CE取得最小值时，∠AFB＝_______°．

Answer 1

【答案】105°

【解析】

如图，作辅助线，构建全等三角形，证明△AEC≌△CFH，得CE＝FH，将CE转化为FH，与BF在同一个三角形中，根据两点之间线段最短，确定点F的位置，即F为AC与BH的交点时，BF＋CE的值最小，求出此时∠AFB＝105°．

解：如图，作CH⊥BC，且CH＝BC，连接BH交AD于M，连接FH，

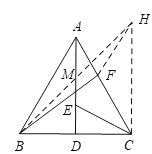
∵△ABC是等边三角形，AD⊥BC，

∴AC＝BC，∠DAC＝30°，

∴AC＝CH，

∵∠BCH＝90°，∠ACB＝60°，

∴∠ACH＝90°60°＝30°，

∴∠DAC＝∠ACH＝30°，

∵AE＝CF，

∴△AEC≌△CFH，

∴CE＝FH，BF＋CE＝BF＋FH，

∴当F为AC与BH的交点时，BF＋CE的值最小，

此时∠FBC＝45°，∠FCB＝60°，

∴∠AFB＝105°，

故答案为：105°.