题目内容
如图是某月的月历.
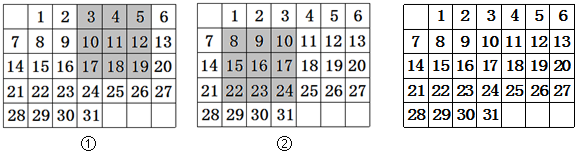
(1)第①图中带阴影的方框中的9个数之和与方框正中心的数有什么关系?若不改变方框大小,将方框移至如②图,还会有第①图同样的关系吗?
(2)不改变带阴影的方框的大小,将方框移动几个位置试一试,你能得出什么结论?你能证明这个结论吗?(提示:用字母表示规律.例如:设9个数其中一个为x)
解:(2)9个数之和为:3+4+5+10+11+12+17+18+19=99,
99÷11=9,
则方框中9个数之和为方框正中心的9倍,
移动位置,9个数字之和为:8+9+10+15+16+17+22+23+24=144,
144÷16=9,
所以改变位置,关系不变;)
(2)不改变带阴影的方框的大小,将方框移动位置,关系不变.
设正中心的数为x,
则9个数之和为:(x-8)+(x-7)+(x-6)+(x-1)+x+(x+1)+(x+6)+(x+7)+(x+8)=9x,
9x÷x=9,
故移动位置,方框中9个数之和为方框正中心的9倍.
分析:(1)求出9个数之和,然后找出与正中心的数的关系为:9个数之和为方框正中心的9倍,改变位置,关系不变;
(2)设正中心的数为x,结合表格依次表示出其他9个数字,然后相加找出关系.
点评:此题考查的是列代数式,解决本题的难点是发现日历中左右相邻的数相隔1,上下相邻的数相隔7.
99÷11=9,
则方框中9个数之和为方框正中心的9倍,
移动位置,9个数字之和为:8+9+10+15+16+17+22+23+24=144,
144÷16=9,
所以改变位置,关系不变;)
(2)不改变带阴影的方框的大小,将方框移动位置,关系不变.
设正中心的数为x,
则9个数之和为:(x-8)+(x-7)+(x-6)+(x-1)+x+(x+1)+(x+6)+(x+7)+(x+8)=9x,
9x÷x=9,
故移动位置,方框中9个数之和为方框正中心的9倍.
分析:(1)求出9个数之和,然后找出与正中心的数的关系为:9个数之和为方框正中心的9倍,改变位置,关系不变;
(2)设正中心的数为x,结合表格依次表示出其他9个数字,然后相加找出关系.
点评:此题考查的是列代数式,解决本题的难点是发现日历中左右相邻的数相隔1,上下相邻的数相隔7.

练习册系列答案
相关题目
 如图是某月的月历.
如图是某月的月历.
 如图是某月的月历,横着取连续的三个数字,它们的和不可能是( )
如图是某月的月历,横着取连续的三个数字,它们的和不可能是( )