题目内容
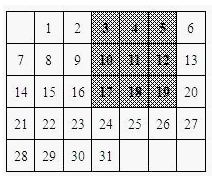
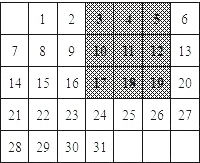 如图是某月的月历,用带阴影的方框任意框九个数.
如图是某月的月历,用带阴影的方框任意框九个数.(1)图中带阴影的方框中的9个数之和与方框正中心的数有什么关系?请说明你的理由?
(2)若这9个数之和是153,写出这9个数,并说明理由.
(3)这9个数之和可能会是100吗?如果可能,请计算出这9个日期,如果不可能,请说明为什么?
分析:(1)设中心的数为x,表示出方框内各数之和,即可得出可得结论;
(2)根据(1)的式子,可解出x,继而可得出这9个数;
(3)令(1)所得的式子为100,解出x的值,看是否为整数即可.
(2)根据(1)的式子,可解出x,继而可得出这9个数;
(3)令(1)所得的式子为100,解出x的值,看是否为整数即可.
解答:解:(1)设中心的数为x,
则(x-8)+(x-7)+(x-6)+(x-1)+(x+1)+(x+6)+(x+7)+(x+8)=9x,
所以9个数之和是方框中心数的9倍;
(2)由题意得,9x=153,
解得:x=17,
所以这9个数为:9、10、11、16、17、18、23、24、25.
(3)若这9个数之和为100,则9x=100,
解得:x=
不为整数,(不符合题意,舍去).
所以不可能.
则(x-8)+(x-7)+(x-6)+(x-1)+(x+1)+(x+6)+(x+7)+(x+8)=9x,
所以9个数之和是方框中心数的9倍;
(2)由题意得,9x=153,
解得:x=17,
所以这9个数为:9、10、11、16、17、18、23、24、25.
(3)若这9个数之和为100,则9x=100,
解得:x=
| 100 |
| 9 |
所以不可能.
点评:本题考查了一元一次方程的应用,解答本题的关键是设出中心的数字,表示出其余的数字,利用方程思想求解,难度一般.

练习册系列答案
相关题目
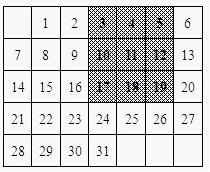
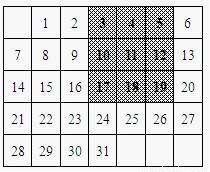
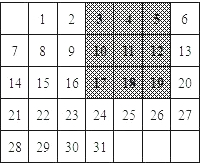 如图是某月的月历,用带阴影的方框任意框九个数.
如图是某月的月历,用带阴影的方框任意框九个数.