题目内容
【题目】已知:在△ABC中,CD⊥AB,∠DEB=∠ACB,∠1+∠2=180°,试判断FG与AB的位置关系,并说明理由.请在下划线内补全解题过程或依据.

解:FG⊥AB,理由如下:
∵∠DEB=∠ACB (已知)
∴AC∥________ (__________________)
∴∠1=∠3(_______________________)
∵∠1+∠2=180°(已知)
∴∠3+∠2=_________(等量代换)
∴FG∥________ (_________________)
∴∠FGA=∠________(_____________)
∵CD⊥AB(已知)
∴∠CDA=90°
∴∠________=90°(等量代换)
∴FG⊥AB(_____________________)
【答案】DE;同位角相等,两直线平行;两直线平行,内错角相等;180°;CD;同旁内角互补,两直线平行;CDA;两直线平行,同位角相等;FGA;垂直的定义.
【解析】
先根据平行线的判定方法,由∠DEB=∠ACB得到AC∥DE,则根据平行线的性质得∠1=∠3,而∠1+∠2=180°,则∠3+∠2=180°,于是可判定FG∥CD,利用∠CDA=90°和平行线性质得∠FGA=∠CDA=90°,于是得到FG⊥AB.
FG⊥AB,理由如下:
∵∠DEB=∠ACB,
∴AC∥DE,(同位角相等,两直线平行)
∴∠1=∠3,(两直线平行,内错角相等)
∵∠1+∠2=180°,
∴∠3+∠2=180°,
∴FG∥CD,(同旁内角互补,两直线平行)
∴∠FGA=∠CDA(两直线平行,同位角相等)
∵CD⊥AB(已知),
∴∠CDA=90°,
∴∠FGA=90°,
∴FG⊥AB(垂直的定义)
故答案为:DE;同位角相等,两直线平行;两直线平行,内错角相等;180°;CD;同旁内角互补,两直线平行;CDA;两直线平行,同位角相等;FGA;垂直的定义.

 字词句段篇系列答案
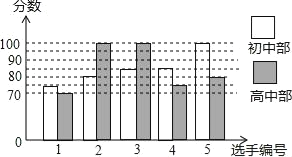
字词句段篇系列答案【题目】某学校举行“中国梦,我的梦”演讲比赛,初、高中部根据初赛成绩,各选出5名选手组成代表队决赛,初、高中部代表队的选手决赛成绩如图所示:
(1)根据图示填写表格:
平均数(分) | 中位数(分) | 众数(分) | |
初中代表队 | 85 |
| 85 |
高中代表队 |
| 80 |
|
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好.