题目内容
【题目】如图(1),![]() 为直线
为直线![]() 上点,过点
上点,过点![]() 作射线
作射线![]() ,
,![]() ,将一直角三角尺(
,将一直角三角尺(![]() )的直角顶点放在点
)的直角顶点放在点![]() 处,一边
处,一边![]() 在射线
在射线![]() 上,另一边
上,另一边![]() 与
与![]() 都在直线
都在直线![]() 的上方.
的上方.
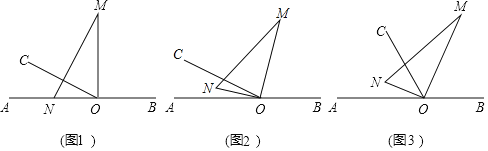
(1)若将图(1)中的三角尺绕点![]() 以每秒
以每秒![]() 的速度,沿顺时针方向旋转
的速度,沿顺时针方向旋转![]() 秒,当
秒,当![]() 恰好平分
恰好平分![]() 时,如图(2).
时,如图(2).
①求![]() 值;
值;
②试说明此时![]() 平分
平分![]() ;
;
(2)将图(1)中的三角尺绕点![]() 顺时针旋转,设
顺时针旋转,设![]() ,
,![]() , 当
, 当![]() 在
在![]() 内部时,试求
内部时,试求![]() 与
与![]() 的数量关系;
的数量关系;
(3)若将图(1)中的三角尺绕点![]() 以每秒
以每秒![]() 的速度沿顺时针方向旋转的同时,射线
的速度沿顺时针方向旋转的同时,射线![]() 也绕点
也绕点![]() 以每秒
以每秒![]() 的速度沿顺时针方向旋转,如图(3),那么经过多长时间,射线
的速度沿顺时针方向旋转,如图(3),那么经过多长时间,射线![]() 第一次平分
第一次平分![]() ?请说明理由.
?请说明理由.
【答案】(1)①t=3s;②证明见解析;(2)β=α+60°;(3)经过5秒OC平分∠MON.
【解析】
(1)①根据角平分线的定义计算即可;
②求出∠AON,∠CON的值即可判断;
(2)根据题意列方程即可得到结论;
(3)设∠AON=5t,∠AOC=30°+8t,根据∠AOC-∠AON=∠CON,构建方程即可解决问题.
解:(1)①如图2中,∵∠AOC=30°,
∴∠BOC=180°-∠AOC=150°,
∵OM平分∠BOC,
∴∠COM=∠BOM=![]() ∠BOC=75°,
∠BOC=75°,
∠AON=180°-90°-75°=15°,
∴t=![]() =3s,
=3s,
②当t=3时,∠AON=3t=15°,∠CON=30°-3t=15°,
∴∠AON=∠CON,
∴ON平分∠AOC;
(2)∵∠CON=30°-α=90°-β,
∴β=α+60°;
(3)∵OC平分∠MON,∠MON=90°,
∴∠CON=∠COM=45°,
∵三角板绕点O以每秒5°的速度,射线OC也绕O点以每秒8°的速度沿顺时针方向旋转一周,
∴设∠AON=5t,∠AOC=30°+8t,
∵∠AOC-∠AON=∠CON,
∴30°+8t-5t=45°,
解得t=5,
∴经过5秒OC平分∠MON.

 考前必练系列答案
考前必练系列答案【题目】为了鼓励市民节约用水,我市居民使用自来水计费方式实施阶梯水价,具体标准见表1,表2分别是小明、小丽、小斌、小宇四家2017年的年用水量和缴纳水费情况.
表1:大连市居民自来水实施阶梯水价标准情况:
阶梯 | 每户年用水量(立方米) | 水价(含污水处理费)(元/立方米) |
第一阶梯 | 0~m(含m) | a |
第二阶梯 | m~240(含240) | 4.40 |
第三阶梯 | 240以上 | 7.85 |
表2:四个家庭2017年的年用水量和缴纳水费情况:
家庭 | 小明 | 小丽 | 小斌 | 小宇 |
用水量(立方米) | 50 | 100 | 200 | 220 |
水费(元) | 162.5 | 325 | 673 | 761 |
请你根据表1、表2提供的数据回答下列问题:
(1)写出表1中的a,m的值;
(2)小颖家2017年使用自来水共缴纳水费827元,则她家2017年的年用水量是多少立方米?