题目内容
古希腊著名的毕达哥拉斯学派把1，3，6，10 ，…这样的数称为“三角形数”（如图①），而把1，4，9，16，…这样的数称为“正方形数”（如图②）．如果规定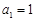
，
，
，
，…；
，
，
，
，…；
，
，
，
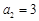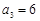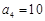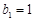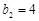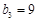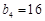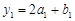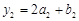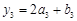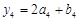，…，那么，按此规定，
，
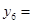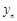＝ （用含n的式子表示，n为正整数）．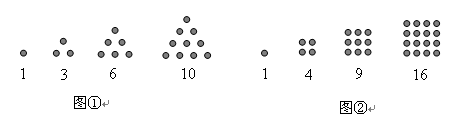
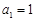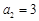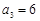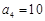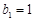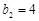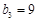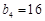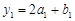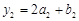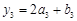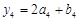，，，，…；，，，，…；，，，，…，那么，按此规定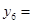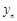， ，＝ （用含n的式子表示，n为正整数）．78，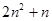
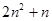
易得a6=1+2+3+…+6，b6=62，把相关数值代入y6的代数式计算即可；同理根据y6的计算方式可得yn的结果．
解答：解：a6=1+2+3+…+6，b6=62，
∴y6=2a6+b6=2×21+36=78；
yn=2an+bn=2×（1+2+3+…+n）+n2=2×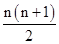
+n2=2n2+n；
故答案为78；2n2+n．
解答：解：a6=1+2+3+…+6，b6=62，
∴y6=2a6+b6=2×21+36=78；
yn=2an+bn=2×（1+2+3+…+n）+n2=2×
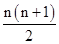+n2=2n2+n；故答案为78；2n2+n．
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
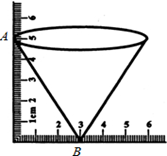
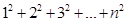．但n为100时，应如何计算正方形的具体个数呢？下面我们就一起来探究并解决这个问题．首先，通过探究我们已经知道
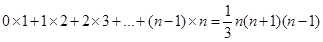时，我们可以这样做：
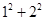=（1+0）×1+（1+1）×2=l+0×1+2+1×2=（1+2）+（0×1+1×2）
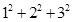=（1+0）×1+（1+1）×2+（l+2）×3
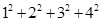=（1+0）×1+（1+1）×2+（l+2）×3+（1+3）×4；
×(___________)
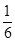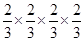写成乘方的形式为＿＿＿＿＿＿＿＿。