题目内容
【题目】为了预防流感,某学校对教室采用药薰消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物燃烧后,y与x成反比例(如图),现测药物8分钟燃毕,此时空气中每立方米含药量为6毫克,请根据题中所提供的信息,回答下列问题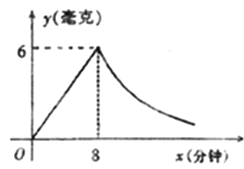
(1)药物燃烧时,y关于x的函数关系式为,自变量x的取值范围是;药物燃烧完后,y与x的函数关系式为;
(2)研究表明,当空气中的每立方米的含药量低于1.6毫克时学生方可进教室,那么从消毒开始,至少需要经过几分钟后,学生才能回到教室;
(3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效地杀灭空气中的病菌,那么此次消毒是否有效?为什么?
【答案】解:(1)∵设正比例函数解析式为y=k1x(k1≠0),函数的图象经过点P(8,6)
∴正比例函数的解析式为![]() .自变量x的取值范围是0≤x≤8;
.自变量x的取值范围是0≤x≤8;
∵设反比例函数解析式为![]() (k2≠0),函数的图象经过点P(8,6),
(k2≠0),函数的图象经过点P(8,6),
∴反比例函数的解析式为![]() . 自变量x的取值范围是x≥4;
. 自变量x的取值范围是x≥4;
(2)把y=1.6代入![]() 中得x=30,
中得x=30,
∴从消毒开始,至少需要经过30分钟后,学生才能回到教室;
(3)把y=3代入![]() 中得x=4,
中得x=4,
把y=3代入![]() 中得x=16,
中得x=16,
(8-4)+(16-8)=12>10,
∴此次消毒是无效的.
【解析】
(1)由于在药物燃烧阶段,y与x成正比例,因此设函数解析式为y=k1x(k1≠0),然后由(8,6)在函数图象上,利用待定系数法即可求得药物燃烧时y与x的函数解析式;由于在药物燃烧阶段后,y与x成反比例,因此设函数解析式为![]() (k2≠0),然后由(8,6)在函数图象上,利用待定系数法即可求得药物燃烧阶段后y与x的函数解析式;
(k2≠0),然后由(8,6)在函数图象上,利用待定系数法即可求得药物燃烧阶段后y与x的函数解析式;
(2)当空气中的每立方米的含药量低于1.6毫克时学生方可进教室,把y=1.6代入![]() ,即可求得y的值,则可求得答案;
,即可求得y的值,则可求得答案;
(3)把y=3代入![]() 中得x=4,把y=3代入
中得x=4,把y=3代入![]() 中得x=16,(8-4)+(16-8)=12>10得知此次消毒是无效的.
中得x=16,(8-4)+(16-8)=12>10得知此次消毒是无效的.

 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案