题目内容
如图,△ABC内接于⊙O,AD⊥BC,OE⊥BC, OE=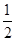 BC.
BC.
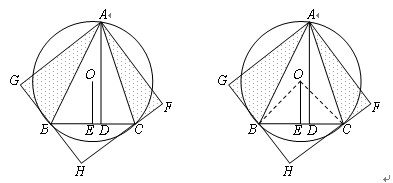
(1)求∠BAC的度数.
(2)将△ACD沿AC折叠为△ACF,将△ABD沿AB折叠为△ABG,延长FC和GB相交于点H.求证:四边形AFHG是正方形.
(3)若BD=6,CD=4,求AD的长.
【答案】
(1)45°
(2)略
(3)12
【解析】(1)解:连结OB和OC.
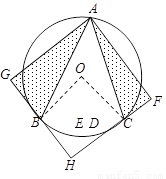
∵ OE⊥BC,∴ BE=CE.
∵ OE=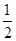 BC,∴ ∠BOC=90°,∴ ∠BAC=45°. ……(2分)
BC,∴ ∠BOC=90°,∴ ∠BAC=45°. ……(2分)
(2)证明:∵ AD⊥BC,∴ ∠ADB=∠ADC=90°.
由折叠可知,AG=AF=AD,∠AGH=∠AFH=90°,
∠BAG=∠BAD,∠CAF=∠CAD, ……(3分)
∴ ∠BAG+∠CAF=∠BAD+∠CAD=∠BAC=45°.
∴ ∠GAF=∠BAG+∠CAF+∠BAC=90°.
∴ 四边形AFHG是正方形. ……(5分)
(3)解:由(2)得,∠BHC=90°,GH=HF=AD,GB=BD=6,CF=CD=4.
设AD的长为x,则 BH=GH-GB=x-6,CH=HF-CF=x-4. ……(7分)
在Rt△BCH中,BH2+CH2=BC2,∴ (x-6)2+(x-4)2=102.
解得,x1=12,x2=-2(不合题意,舍去).
∴ AD=12. ……(8分)

练习册系列答案
相关题目
 15、如图,△ABC内接于⊙O,∠BAC=120°,AB=AC=4.BD为⊙O的直径,则BD=
15、如图,△ABC内接于⊙O,∠BAC=120°,AB=AC=4.BD为⊙O的直径,则BD= 21、如图,△ABC内接于⊙O,AB为⊙O的直径,点D在AB的延长线上,∠A=∠D=30°.
21、如图,△ABC内接于⊙O,AB为⊙O的直径,点D在AB的延长线上,∠A=∠D=30°.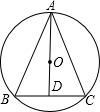 已知:如图,△ABC内接于⊙O,连接AO并延长交BC于点D,若AO=5,BC=8,∠ADB=90°,求△ABC的面积.
已知:如图,△ABC内接于⊙O,连接AO并延长交BC于点D,若AO=5,BC=8,∠ADB=90°,求△ABC的面积. 18、如图,△ABC内接于⊙O,∠A=30°,若BC=4cm,则⊙O的直径为( )
18、如图,△ABC内接于⊙O,∠A=30°,若BC=4cm,则⊙O的直径为( ) 如图,△ABC内接于⊙O,AD⊥BC于点D,求证:∠BAD=∠CAO.
如图,△ABC内接于⊙O,AD⊥BC于点D,求证:∠BAD=∠CAO.