题目内容
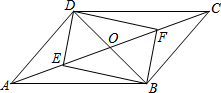 如图,平行四边形ABCD中,对角线AC,BD相交于点O,若E、F是AC上两动点,E、F分别从A、C两点同时以1cm/s的相同的速度向C、A运动.
如图,平行四边形ABCD中,对角线AC,BD相交于点O,若E、F是AC上两动点,E、F分别从A、C两点同时以1cm/s的相同的速度向C、A运动.(1)四边形DEBF是平行四边形吗?说明你的理由.
(2)若BD=10cm,AC=16cm,当运动时间t为多少时,四边形DEBF为矩形.
考点:平行四边形的判定与性质,矩形的判定
专题:几何图形问题,数形结合,方程思想
分析:(1)由平行四边形ABCD中,可得OA=OC,OB=OD,又由若E、F是AC上两动点,E、F分别从A、C两点同时以1cm/s的相同的速度向C、A运动,易得AE=CF,即可得OE=OF,则可判定四边形DEBF是平行四边形;
(2)由四边形DEBF是平行四边形,可得当EF=BD时,四边形DEBF为矩形,即可得方程:16-t-t=10,继而求得答案.
(2)由四边形DEBF是平行四边形,可得当EF=BD时,四边形DEBF为矩形,即可得方程:16-t-t=10,继而求得答案.
解答:解:(1)四边形DEBF是平行四边形.
理由:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵E、F是AC上两动点,E、F分别从A、C两点同时以1cm/s的相同的速度向C、A运动,
∴AE=CF,
∴OE=OF,
∴四边形DEBF是平行四边形;
(2)根据题意得:AE=CF=tcm,
∵四边形DEBF是平行四边形,
∴当EF=BD时,四边形DEBF为矩形.
即AC-AE-CF=BD,
∴16-t-t=10,
解得:t=3,
∴当运动时间t为3s时,四边形DEBF为矩形.
理由:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵E、F是AC上两动点,E、F分别从A、C两点同时以1cm/s的相同的速度向C、A运动,
∴AE=CF,
∴OE=OF,
∴四边形DEBF是平行四边形;
(2)根据题意得:AE=CF=tcm,
∵四边形DEBF是平行四边形,
∴当EF=BD时,四边形DEBF为矩形.
即AC-AE-CF=BD,
∴16-t-t=10,
解得:t=3,
∴当运动时间t为3s时,四边形DEBF为矩形.
点评:此题考查了平行四边形的判定与性质以及矩形的判定.此题难度适中,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
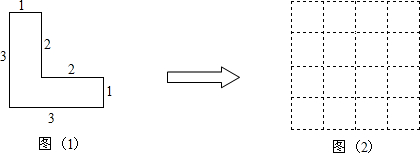
 如图,现有一张正方形纸片ABCD,点P为正方形AD边上的一点(不与点A、点D重合),将正方形纸片折叠,使点C落在P处,点B落在O处,OP交AB于Q,折痕为MN,连接CP.
如图,现有一张正方形纸片ABCD,点P为正方形AD边上的一点(不与点A、点D重合),将正方形纸片折叠,使点C落在P处,点B落在O处,OP交AB于Q,折痕为MN,连接CP. 如图,在△ABC中,AB=AC=8cm,D是BC上任意一点,DE∥AB,DF∥AC,F、E分别在AB、AC上,则平行四边形AFDE的周长为
如图,在△ABC中,AB=AC=8cm,D是BC上任意一点,DE∥AB,DF∥AC,F、E分别在AB、AC上,则平行四边形AFDE的周长为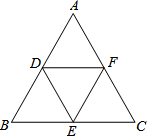 如图,已知D、E、F分别为△ABC的中点,则四边形DECF为
如图,已知D、E、F分别为△ABC的中点,则四边形DECF为