题目内容
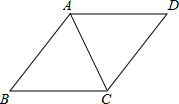（2012•黄埔区一模）如图，AC是平行四边形ABCD的对角线，∠ACB=∠ACD．求证：AB=AD．
分析：根据平行四边形的对角相等可得∠B=∠D，然后利用“角角边”证明△ACD和△ACB全等，再根据全等三角形对应边相等即可证明．
解答：证明：∵四边形ABCD平行四边形（已知），
∴∠B=∠D（平行四边形对角相等），…（3分）
在△ADC和△ABC中
，
∴△ACD≌△ACB（AAS），…8
∴△AB=AD（全等三角形对应边相等）．…（9分）
∴∠B=∠D（平行四边形对角相等），…（3分）
在△ADC和△ABC中
|
∴△ACD≌△ACB（AAS），…8
∴△AB=AD（全等三角形对应边相等）．…（9分）
点评：本题考查了平行四边形的对角相等的性质，全等三角形的判定与性质，是基础题，熟记性质与全等三角形的判定方法是解题的关键．
练习册系列答案
相关题目
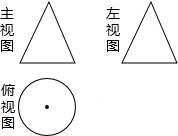（2012•黄埔区一模）一个几何体的三视图如右图所示，这个几何体是（ ）
（2012•黄埔区一模）如图，边长为4的等边△ABC中，DE为中位线，则四边形BCED的周长为（ ）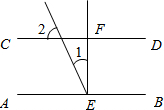
（2012•黄埔区一模）如图，AB∥CD，EF⊥AB于E，EF交CD于F，已知∠1=30°，则∠2=（ ）