题目内容
【题目】如图,已知:AB//CD,求证:![]() B+
B+![]() D+
D+![]() BED=360°(至少用三种方法)
BED=360°(至少用三种方法)
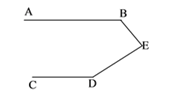
【答案】证明见解析
【解析】试题分析:(1)连接BD,构造三角形BDE,利用三角形内角和是180°平行线同旁内角互补可证明.(2) 延长DE交AB延长线于F,构造三角形BEF,利用三角形外角定理和同旁内角互补证明.(3) 过点E作EF//AB,利用同旁内角互补证明.
试题解析:
证明:(1)连结BD,如图
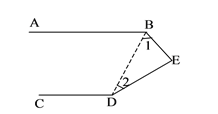
∵AB![]() ,∠ABD+∠CDB=180°,
,∠ABD+∠CDB=180°,
∵∠1+∠2+∠BED=180°,
∴∠ABD+∠1+∠CDE+∠BED=360°.
(2)延长DE交AB延长线于F,如图
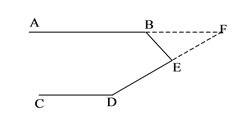
∵AB![]()
∴∠F+∠D=180°,
∵∠ABE=∠FEB+∠F,
∠BED=∠FBE+∠F,
∴∠ABE+∠CDE+∠BED=∠FEB+∠F+∠CDE+∠FBE+∠F=180°+180°=360°.
(3)过点E作EF//AB,如图
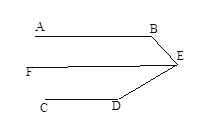
∵AB![]()
∴AB![]() ,
,
∴∠B+∠BEF=180°,
∠D+∠DEF=180°,
所以∠B+∠BEF+∠D+∠DEF=180°+180°=360°,
∴∠B+∠D+∠BED=360°.

练习册系列答案
相关题目