��Ŀ����
����Ŀ����֪���� OC �ڡ�AOB ���ڲ������� OE ƽ�֡�AOC������ OF ƽ�֡�COB��
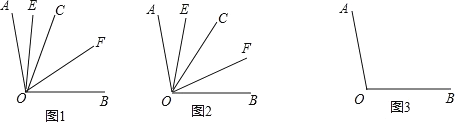
��1����ͼ 1������AOB=100������AOC=32�������EOF= �ȣ�
��2������AOB=������AOC=����
����ͼ 2�������� OC �ڡ�AOB ���ڲ��Ƶ� O ��ת�����EOF �Ķ�����
�������� OC �ڡ�AOB ���ⲿ�Ƶ� O ��ת(��ת�С�AOC����BOC ����ָС�� 180���Ľ�)�������������䣬�����ͼ 3 ̽����EOF �Ĵ�С��ֱ��д����EOF �Ķ�����
���𰸡���50�㣻�Ƣ� ![]() ������
������ ![]() ���� 180��-
���� 180��-![]() ��.
��.
��������
��1���������BOC���������ݽ�ƽ���߶��������EOC�͡�FOC��������ͼ��ɵó�����
��2�������ݽ�ƽ���߶���ó���COE![]() ��AOC����COF
��AOC����COF![]() ��BOC�������EOF����EOC+��FOC
��BOC�������EOF����EOC+��FOC![]() ��AOB���������������
��AOB���������������
�������������a������OE��OFֻ��1���ڡ�AOB���������ݽ�ƽ���߶���ó���COE![]() ��AOC����COF
��AOC����COF![]() ��BOC�������EOF����FOC����COE
��BOC�������EOF����FOC����COE![]() ��AOB��
��AOB��
b������OE��OF2�����ڡ�AOB���������ݽ�ƽ���߶���ó���EOF![]() ��AOC����COF
��AOC����COF![]() ��BOC�������EOF����EOC+��COF
��BOC�������EOF����EOC+��COF![]() ��360�㩁��AOB�����������������
��360�㩁��AOB�����������������
��1���ߡ�AOB��100�㣬��AOC��32�㣬���BOC����AOB����AOC��68�㣮
��OE��OF�ֱ��ǡ�AOC�͡�COB�Ľ�ƽ���������EOC![]() ��AOC��16�㣬��FOC
��AOC��16�㣬��FOC![]() ��BOC��34�㣬���EOF����EOC+��FOC��16��+34�㣽50�㣻
��BOC��34�㣬���EOF����EOC+��FOC��16��+34�㣽50�㣻
��2���١�OE��OF�ֱ��ǡ�AOC�͡�COB�Ľ�ƽ���������EOC![]() ��AOC����FOC
��AOC����FOC![]() ��BOC�����EOF����EOC+��FOC
��BOC�����EOF����EOC+��FOC![]() ��AOB
��AOB![]() ����
����
�����������������a������OE��OFֻ��1���ڡ�AOB��������ͼ3������EOF����FOC����COE![]() ��BOC
��BOC![]() ��AOC
��AOC![]() ����BOC����AOC��
����BOC����AOC��![]() ��AOB=
��AOB=![]() ����
����
b������OE��OF2�����ڡ�AOB��������ͼ3������EOF����EOC+��COF![]() ��AOC
��AOC![]() ��BOC
��BOC![]() ����AOC+��BOC��
����AOC+��BOC��![]() ��360�㩁��AOB��180�㣭
��360�㩁��AOB��180�㣭![]() ��AOB=180�㣭
��AOB=180�㣭![]() ����
����
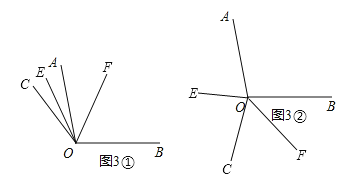
�ʡ�EOF�Ķ�����![]() ����180�㣭
����180�㣭![]() ����
����

 53���ò�ϵ�д�
53���ò�ϵ�д�