Question

【题目】图1是由若干个小圆圈堆成的一个形如等边三角形的图案，最上面一层有一个圆圈，

以下各层均比上一层多一个圆圈，一共堆了n 层. 将图1倒置后与原图1拼成图2的形状，这样我们可以

算出图1中所有圆圈的个数为1＋2＋3＋…＋n＝.

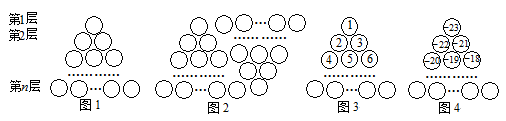
如果图中的圆圈共有13层，请解决下列问题：

(1)我们自上往下，在每个圆圈中按图3的方式填上一串连续的正整数1， 2，3，4，……，则最底层最左边这个圆圈中的数是 ；

(2)我们自上往下，在每个圆圈中按图4的方式填上一串连续的整数－23，－22，－21，－20，……，求最底层最右边圆圈内的数是_______；

(3)求图4中所有圆圈中各数的绝对值之和.

Answer 1

【答案】(1)79；(2)67；(3)2554

【解析】

试题分析：(1)第13层的第一个数字等于第12层的最后一个数字加1，首先根据公式求出第12层的最后一个数字，然后进行计算；(2)方法同(1)；(3)求出最后一个数字，然后根据图中给出的方法进行计算.

试题解析：(1)12×(12+1)÷2=78 78+1=79

(2)－23+79－1=55 55+12=67

(3)(1+2+3+4+…+23)×2+24+25+…+67=2554