题目内容
【题目】如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE. 
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.
【答案】
(1)证明:∵△BAD是由△BEC在平面内绕点B旋转60°而得,
∴DB=CB,∠ABD=∠EBC,∠ABE=60°,
∵AB⊥EC,
∴∠ABC=90°,
∴∠DBE=∠CBE=30°,
在△BDE和△BCE中,
∵ 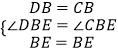 ,
,
∴△BDE≌△BCE
(2)四边形ABED为菱形;
由(1)得△BDE≌△BCE,
∵△BAD是由△BEC旋转而得,
∴△BAD≌△BEC,
∴BA=BE,AD=EC=ED,
又∵BE=CE,
∴四边形ABED为菱形
【解析】(1)根据旋转的性质可得DB=CB,∠ABD=∠EBC,∠ABE=60°,然后根据垂直可得出∠DBE=∠CBE=30°,继而可根据SAS证明△BDE≌△BCE;(2)根据(1)以及旋转的性质可得,△BDE≌△BCE≌△BDA,继而得出四条棱相等,证得四边形ABED为菱形.

练习册系列答案
相关题目