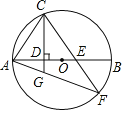
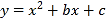题目内容
【题目】如图,在平面直角坐标系中,点![]() 是原点,矩形
是原点,矩形![]() 的顶点
的顶点![]() 在
在![]() 轴的正半轴上,顶点
轴的正半轴上,顶点![]() 在
在![]() 轴的正半轴上,顶点
轴的正半轴上,顶点![]() 的坐标为
的坐标为![]() ,抛物线
,抛物线![]() 经过
经过![]() ,
,![]() 两点,与
两点,与![]() 轴的另一个交点为点
轴的另一个交点为点![]() .
.
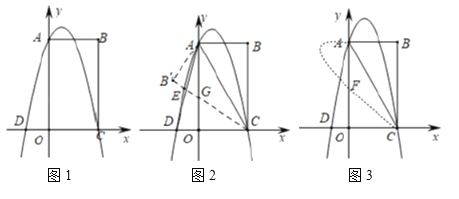
(1)如图1,求抛物线的函数表达式;
(2)如图2,连接![]() ,
,![]() ,将
,将![]() 沿
沿![]() 折叠后与
折叠后与![]() 、
、![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,求
,求![]() 的长度;
的长度;
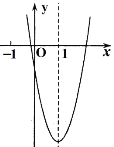
(3)如图3,将抛物线在![]() 上方的部分沿
上方的部分沿![]() 折叠后与
折叠后与![]() 轴交于点
轴交于点![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据矩形性质分析出![]() ,
,![]() ,然后用待定系数法求函数解析式;(2)由折叠的性质可得
,然后用待定系数法求函数解析式;(2)由折叠的性质可得![]() ,然后结合全等三角形的性质,平行线的性质及等腰三角形的判定得到
,然后结合全等三角形的性质,平行线的性质及等腰三角形的判定得到![]() .设
.设![]() ,则
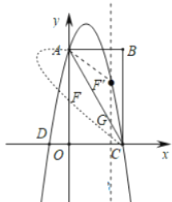
,则![]() ,利用勾股定理列方程求解;(3)在AC上方的抛物线图象取点F的对称点F′,过点F′作y轴的平行线交直线AC于点G.先证F′A=F′G.继而得直线AC的解析式为y=-2x+4.设点F(n,-2n2+2n+4),则G(n,-2n+4).根据F′A2=F′G2求出n的值,从而得出FG=
,利用勾股定理列方程求解;(3)在AC上方的抛物线图象取点F的对称点F′,过点F′作y轴的平行线交直线AC于点G.先证F′A=F′G.继而得直线AC的解析式为y=-2x+4.设点F(n,-2n2+2n+4),则G(n,-2n+4).根据F′A2=F′G2求出n的值,从而得出FG=![]() ,F′A=F′G=FA=
,F′A=F′G=FA=![]() ,从而得出点F的坐标.
,从而得出点F的坐标.
解:(1)![]() 四边形
四边形![]() 是矩形,
是矩形,![]() ,
,
![]() ,
,![]() ,
,
![]() 抛物线
抛物线![]() 经过
经过![]() ,
,![]() 两点,
两点,
![]()
![]()
![]() 抛物线的函数表达式为
抛物线的函数表达式为![]() .
.
(2)由题意得:![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
设![]() ,则
,则![]() .
.
在![]() 中,
中,![]()
解得![]() ,
,
![]() .
.
(3)如图,在![]() 上方的抛物线上取点
上方的抛物线上取点![]() 的对称点
的对称点![]() ,过点
,过点![]() 作
作![]() 轴的平行线交直线
轴的平行线交直线![]() 于点
于点![]() .
.
由题意得:![]() ,
,![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
易得直线![]() 的解析式为:
的解析式为:![]() .
.
设点![]() ,则
,则![]()
![]() ,
,![]() .
.
![]() ,
,
![]() ,
,
即:![]() ,
,
化简得:![]() ,即
,即![]() ,
,
解得![]() (不合题意,舍去)或
(不合题意,舍去)或![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()

练习册系列答案
相关题目