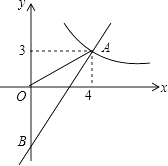题目内容
【题目】如图,已知二次函数图象的对称轴为直线x=2,顶点为点C,直线y=x+m与该二次函数的图象交于点A,B两点,其中点A的坐标为(5,8),点B在y轴上.
(1)求m的值和该二次函数的表达式.P为线段AB上一个动点(点P不与A,B两点重合),过点P作x轴的垂线,与这个二次函数的图象交于点E.
①设线段PE的长为h,求h与x之间的函数关系式,并写出自变量x的取值范围.
②若直线AB与这个二次函数图象的对称轴的交点为D,求当四边形DCEP是平行四边形时点P的坐标.
(2)若点P(x,y)为直线AB上的一个动点,试探究:以PB为直径的圆能否与坐标轴相切?如果能请求出点P的坐标,如果不能,请说明理由.
【答案】
(1)解: A的坐标为(5,8)在直线y=x+m上,
∴8=5+m,
∴m=3,
∴直线AB解析式为y=x+3,
∴B(0,3),
设抛物线解析式为y=a(x﹣2)2+k,
∵点A,B在抛物线上,
∴ ![]() ,
,
∴ ![]() ,
,
∴抛物线解析式为y=(x﹣2)2﹣1=x2﹣4x+3,顶点C(2,﹣1)
①∵点P在线段AB上,
∴P(x,x+3)(0≤x≤5),
∵PE⊥x轴,交抛物线与E,P(x,x+3),
∴E(x,x2﹣4x+3),
∴h=PE=x+3﹣(x2﹣4x+3)=﹣x2+5x,(0≤x≤5)
②∵直线AB与这个二次函数图象的对称轴的交点为D,
∴D(2,5),
∴DC=6,
∵四边形DCEP是平行四边形,
∴PE=DC=6,
∵PE=|﹣x2+5x|,
Ⅰ、当0≤x≤5时,﹣x2+5x=6,
∴x1=2(舍),x2=3,
∴P(3,6),
Ⅱ、当x<0,或x>5时,x2﹣5x=6,
∴x3=﹣1,x4=6,
∴P(﹣1,2)或P(6,9),(舍)
即:点P的坐标为(3,6)
(2)解:∵点P(x,y)为直线AB上的一个动点,
∴P(x,x+3),
∴点P到x轴的距离为|x+3|,到y轴的距离为|x|,
∵点B(0,3),
∴BP= ![]() |x|,
|x|,
∵以PB为直径的圆能与坐标轴相切,
∴①以PB为直径的圆能与y轴相切,
∴|x|= ![]() |x|,
|x|,
∴x=0(舍),
②以PB为直径的圆能与x轴相切,
∴|x+3|= ![]() |x|,
|x|,
∴x=﹣6﹣3 ![]() 或x=﹣6+3
或x=﹣6+3 ![]() ,
,
∴P(﹣6﹣3 ![]() ,﹣3+3
,﹣3+3 ![]() )或P(﹣6﹣3
)或P(﹣6﹣3 ![]() ,﹣3﹣3
,﹣3﹣3 ![]() ).
).
故存在点P,坐标为P(﹣6+3 ![]() ,﹣3+3
,﹣3+3 ![]() )或P(﹣6﹣3
)或P(﹣6﹣3 ![]() ,﹣3﹣3
,﹣3﹣3 ![]() )时,以PB为直径的圆能与坐标轴相切
)时,以PB为直径的圆能与坐标轴相切
【解析】(1)易由点A的坐标为(5,8)可得直线AB解析式为y=x+3;从而求得B(0,3),结合对称轴直线x=2,可利用顶点式求得抛物线解析式,顶点C为(2,﹣1)。①从而PE的长为两个函数的差PE=x+3﹣(x2﹣4x+3)=﹣x2+5x,(0≤x≤5)②易得直线AB与这个二次函数图象的对称轴的交点为D,点D坐标易得为(2,5),由四边形DCEP是平行四边形,PE=DC=6,由①中的函数解析式可得当0≤x≤5时,﹣x2+5x=6;当x<0,或x>5时,x2﹣5x=6计算得到点P的坐标为(3,6)
(2)由点P(x,y)为直线AB上的一个动点,可得P(x,x+3)所以点P到x轴的距离为|x+3|,到y轴的距离为|x|,由点B可得BP的长,可判断能与坐标轴相切;分类讨论与x轴或Y轴两种情况,可得最后结果及P取何值时可相切。

 阅读快车系列答案
阅读快车系列答案