题目内容
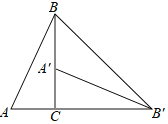
【题目】如图,E是边长为1的正方形ABCD的对角线BD上一动点,点E从点B向点D运动(与点B,D不重合),过点E作直线GH∥BC,交AB于点G,交CD于点H,EF⊥AE,交CD(或CD的延长线)于点F.
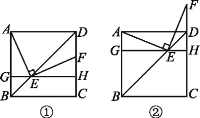
(1)如图①,求证:△AGE≌△EHF.
(2)在点E的运动过程中(如图①,②),四边形AFHG的面积是否会发生变化?请说明理由.
【答案】(1)见解析;(2)四边形AFHG的面积不会发生变化,都是![]() ;理由见解析.
;理由见解析.
【解析】
(1)根据四边形ABCD是正方形,BD是对角线,且GH∥BC可证明AGHD是矩形,∠AGE=∠EHF=90°,AG=DH,△GBE是等腰直角三角形,可得DH=HE,即可证明AG=EH,利用EF⊥AE及直角三角形两锐角互余的关系可得∠AEG=∠EFH,根据AAS即可证明△AGE≌△EHF;
(2)分两种情况进行讨论:①当点E运动到BD的中点时,可得四边形AFHG是矩形,可得S四边形AFHG=![]() ;②当点E不在BD的中点时,点E在运动(与点B、D不重合)的过程中,四边形AFHG是直角梯形,由(1)知,△AGE≌△EHF,图②时,同(1)的证明方法可得△AGE≌△EHF,S四边形AFHG=
;②当点E不在BD的中点时,点E在运动(与点B、D不重合)的过程中,四边形AFHG是直角梯形,由(1)知,△AGE≌△EHF,图②时,同(1)的证明方法可得△AGE≌△EHF,S四边形AFHG=![]() (FH+AG)GH=
(FH+AG)GH=![]() ,然后即可得出结论.
,然后即可得出结论.
(1)∵四边形ABCD是正方形,GH∥BC,
∴AGHD是矩形,
∴∠AGE=∠EHF=90°,AG=DH,
∵BD是对角线,
∴∠HDE=45°,
∴△EHD是等腰直角三角形,
∴DH=HE,
∴AG=EH.
∵EF⊥AE,
∴∠AEG+∠FEH=90°.
∵∠EFH+∠FEH=90°,
∴∠AEG=∠EFH.
在△AGE和△EHF中,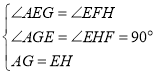 ,
,
∴△AGE≌△EHF(AAS).
(2)四边形AFHG的面积不会发生变化.
理由:①当E运动到BD的中点时,F与D重合,
∴四边形AFHG是矩形,
∵E为BD中点,GH//BC,
∴DH=![]() CD=
CD=![]() ,
,
∴S四边形AFHG=![]() ,
,
②当E不在BD的中点时,在点E的运动(与点B、D不重合)过程中,四边形AFHG是直角梯形.
由(1)知图①中△AGE≌△EHF,
如图②,∵ABCD是正方形,GH//BC,
∴AGHD是矩形,
∴AG=HD,∠AGE=∠EHF=90°,
∵E在对角线BD上,
∴∠EDH=45°,
∴△EDH是等腰直角三角形,
∴EH=HD,
∴AG=EH,
∵EF⊥AE,
∴∠AEG+∠FEH=90°,
∵∠F+∠FEH=90°,
∴∠AEG=∠F,
在△AGE和△EHF中,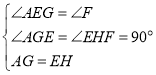 ,
,
∴△AGE≌△EHF(AAS).
∴FH=EG=BG,
∴FH+AG=BG+AG=AB=1.
∴S四边形AFHG=![]() (FH+AG)·GH=
(FH+AG)·GH=![]() .
.
综上所述,四边形AFHG的面积不会发生变化,都是![]() .
.

 学业测评一课一测系列答案
学业测评一课一测系列答案