题目内容
【题目】如图,等腰△ABC如图放置,顶角的顶点C在直线m上,分别过点A、B作直线m的垂线,垂足分别为E、D,且AE=CD.
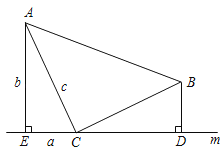
(1)求证:△AEC≌△CDB;
(2)若设△AEC的三边长分別为a、b、c,利用此图证明勾股定理.
【答案】(1)详见解析;(2)详见解析
【解析】
(1)通过直角三角形两锐角互余证明∠CAE=∠BCD ,再证得△CAE≌△BCD,
(2)利用等面积法证得勾股定理.
(1)证明:∵∠ACB=90°,
∴∠ACE+∠BCD=90°.
∵∠ACE+∠CAE=90°,
∴∠CAE=∠BCD.
在△AEC与△BCD中,
 ,
,
∴△CAE≌△BCD(AAS).
(2)解:由①知:△CAE≌△BCD,
∴BD=CE=a,CD=AE=b,
∴S梯形AEDB=![]()
又∵S梯形AEDB=S△AEC+S△BCD+S△ABC
![]()
∴![]()
整理,得a2+b2=c2.

练习册系列答案
相关题目