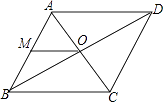
题目内容
【题目】已知直线![]() 与抛物线
与抛物线![]() 有一个公共点
有一个公共点![]() ,且
,且![]() .
.
(Ⅰ)求抛物线顶点![]() 的坐标(用含
的坐标(用含![]() 的代数式表示);
的代数式表示);
(Ⅱ)说明直线与抛物线有两个交点;
(Ⅲ)直线与抛物线的另一个交点记为![]() .
.
(ⅰ)若![]() ,求线段
,求线段![]() 长度的取值范围;
长度的取值范围;
(ⅱ)求![]() 面积的最小值.
面积的最小值.
【答案】(Ⅰ)抛物线顶点Q的坐标为(-![]() ,-
,-![]() );(Ⅱ)理由见解析;
);(Ⅱ)理由见解析;
(Ⅲ)(i)5![]() ≤MN≤7
≤MN≤7![]() .(ii)△QMN面积的最小值为
.(ii)△QMN面积的最小值为![]() .
.
【解析】
试题分析:(Ⅰ)由抛物线过点M(1,0),可得b=-2a,将解析式y=ax2+ax+b=ax2+ax-2a配方得y=a(x+ ![]() )2-
)2- ![]() ,从而可得抛物线顶点Q的坐标为(-
,从而可得抛物线顶点Q的坐标为(- ![]() ,-
,- ![]() ).
).
(Ⅱ)由直线y=2x+m经过点M(1,0),可得m=-2.
由y=2x-2、y=ax2+ax-2a,可得ax2+(a-2)x-2a+2=0,(*),由根的判别式可得方程(*)有两个不相等的实数根,从而可得直线与抛物线有两个交点.
(Ⅲ)由y=2x-2、y=ax2+ax-2a,可得点N(![]() -2,
-2,![]() -6).
-6).
(i)根据勾股定理得,MN2=20(![]() )2,再由-1≤a≤-
)2,再由-1≤a≤-![]() ,可得-2≤
,可得-2≤![]() ≤-1,从而可得
≤-1,从而可得![]() <0,
<0,
继而可得MN=3![]() ,从而可得MN的取值范围.
,从而可得MN的取值范围.
(ii)作直线x=-![]() 交直线y=2x-2于点E,得 E(-
交直线y=2x-2于点E,得 E(-![]() ,-3),
,-3),
从而可得△QMN的面积S=S△QEN+S△QEM =![]() ,即27a2+(8S-54)a+24=0,(*)
,即27a2+(8S-54)a+24=0,(*)
因为关于a的方程(*)有实数根, 从而可和S≥![]() ,继而得到面积的最小值.
,继而得到面积的最小值.
试题解析:(Ⅰ)因为抛物线过点M(1,0),所以a+a+b=0,即b=-2a,所以y=ax2+ax+b=ax2+ax-2a=a(x+![]() )2-
)2-![]() ,所以抛物线顶点Q的坐标为(-
,所以抛物线顶点Q的坐标为(-![]() ,-
,-![]() ).
).
(Ⅱ)因为直线y=2x+m经过点M(1,0),所以0=2×1+m,解得m=-2.
把y=2x-2代入y=ax2+ax-2a,得ax2+(a-2)x-2a+2=0,(*),所以△=(a-2)2-4a(-2a+2)=9a2-12a+4由(Ⅰ)知b=-2a,又a<b,所以a<0,b>0,所以△>0,所以方程(*)有两个不相等的实数根,故直线与抛物线有两个交点.
(Ⅲ)把y=2x-2代入y=ax2+ax-2a,得ax2+(a-2)x-2a+2=0,
即x2+(1-![]() )x-2+
)x-2+![]() =0,所以(x-1)(x+2-
=0,所以(x-1)(x+2-![]() )=0,
)=0,
解得x1=1,x2 =![]() -2,所以点N(
-2,所以点N(![]() -2,
-2,![]() -6).
-6).
(i)根据勾股定理得,MN2=[(![]() -2)-1]2+(
-2)-1]2+(![]() -6)2=20(
-6)2=20(![]() )2,
)2,
因为-1≤a≤-![]() ,由反比例函数性质知-2≤
,由反比例函数性质知-2≤![]() ≤-1,所以
≤-1,所以![]() <0,
<0,
所以MN=2![]() (
(![]() )=3
)=3![]() ,所以5
,所以5![]() ≤MN≤7
≤MN≤7![]() .
.
(ii)作直线x=-![]() 交直线y=2x-2于点E,把x=-
交直线y=2x-2于点E,把x=-![]() 代入y=2x-2得,y=-3,即E(-
代入y=2x-2得,y=-3,即E(-![]() ,-3),
,-3),
又因为M(1,0),N(![]() -2,
-2,![]() -6),且由(Ⅱ)知a<0,
-6),且由(Ⅱ)知a<0,
所以△QMN的面积S=S△QEN+S△QEM=![]() =
=![]() ,
,
即27a2+(8S-54)a+24=0,(*)
因为关于a的方程(*)有实数根,所以△=(8S-54)2-4×27×24≥0,即(8S-54)2≥(36![]() )2,
)2,
又因为a<0,所以S=![]() >
>![]() ,所以8S-54>0,所以8S-54>0,
,所以8S-54>0,所以8S-54>0,
所以8S-54≥36![]() ,即S≥
,即S≥![]() ,
,
当S=![]() 时,由方程(*)可得a=-
时,由方程(*)可得a=-![]() 满足题意.
满足题意.
故当a=-![]() ,b =
,b =![]() 时,△QMN面积的最小值为
时,△QMN面积的最小值为![]() .
.