Question

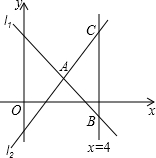
已知直线l₁：y=-x+3与过点(3，

5

2

)和点（-2，-5）的直线l₂相交于点A，直线x=4与直线l₁和直线l₂分别相交于点B、C．
（1）求直线l₂的解析式和点A的坐标；
（2）求△ABC的面积．

Answer 1

（1）设直线l₂的解析式为y=kx+b，
则

3k+b= 5 2 -2k+b=-5

，
解得

k= 3 2 b=-2

，
所以直线l₂的解析式为y=

3

2

x-2；
联立

y=-x+3 y= 3 2 x-2

，
解得

x=2 y=1

，
所以点A的坐标为（2，1）；

（2）当x=4时，y=-4+3=-1，
y=4×

3

2

-2=6-2=4，
所以点B（4，-1），C（4，4），
所以BC=4-（-1）=4+1=5，
点A到BC的距离为4-2=2，
所以S_△ABC=

1

2

×5×2=5．