题目内容
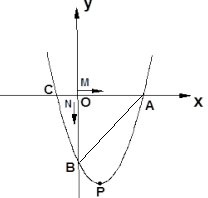
如图,在Rt△ABO中,斜边AB=1.若OC∥BA,∠AOC=36°,则
- A.点B到AO的距离为sin54°
- B.点B到AO的距离为tan36°
- C.点A到OC的距离为sin36°sin54°
- D.点A到OC的距离为cos36°sin54°
C
分析:根据图形得出B到AO的距离是指BO的长,过A作AD⊥OC于D,则AD的长是点A到OC的距离,根据锐角三角形函数定义得出BO=ABsin36°,即可判断A、B;过A作AD⊥OC于D,则AD的长是点A到OC的距离,根据锐角三角形函数定义得出AD=AOsin36°,AO=AB•sin54°,求出AD,即可判断C、D.
解答: 解:
解:
A、B到AO的距离是指BO的长,
∵AB∥OC,
∴∠BAO=∠AOC=36°,
∵在Rt△BOA中,∠BOA=90°,AB=1,
∴sin36°=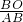 ,
,
∴BO=ABsin36°=sin36°,
故本选项错误;
B、由以上可知,选项错误;
C、过A作AD⊥OC于D,则AD的长是点A到OC的距离,
∵∠BAO=36°,∠AOB=90°,
∴∠ABO=54°,
∵sin36°=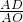 ,
,
∴AD=AO•sin36°,
∵sin54°= ,
,
∴AO=AB•sin54°,
∵AB=1,
∴AD=AB•sin54°•sin36°=1×sin54°•sin36°=sin54°•sin36°,故本选项正确;
D、由以上可知,选项错误;
故选C.
点评:本题考查了对解直角三角形和点到直线的距离的应用,解此题的关键是①找出点A到OC的距离和B到AO的距离,②熟练地运用锐角三角形函数的定义求出关系式,题目较好,但是一道比较容易出错的题目.
分析:根据图形得出B到AO的距离是指BO的长,过A作AD⊥OC于D,则AD的长是点A到OC的距离,根据锐角三角形函数定义得出BO=ABsin36°,即可判断A、B;过A作AD⊥OC于D,则AD的长是点A到OC的距离,根据锐角三角形函数定义得出AD=AOsin36°,AO=AB•sin54°,求出AD,即可判断C、D.
解答:
 解:
解:A、B到AO的距离是指BO的长,
∵AB∥OC,
∴∠BAO=∠AOC=36°,
∵在Rt△BOA中,∠BOA=90°,AB=1,
∴sin36°=
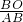 ,
,∴BO=ABsin36°=sin36°,
故本选项错误;
B、由以上可知,选项错误;
C、过A作AD⊥OC于D,则AD的长是点A到OC的距离,
∵∠BAO=36°,∠AOB=90°,
∴∠ABO=54°,
∵sin36°=
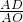 ,
,∴AD=AO•sin36°,
∵sin54°=
 ,
,∴AO=AB•sin54°,
∵AB=1,
∴AD=AB•sin54°•sin36°=1×sin54°•sin36°=sin54°•sin36°,故本选项正确;
D、由以上可知,选项错误;
故选C.
点评:本题考查了对解直角三角形和点到直线的距离的应用,解此题的关键是①找出点A到OC的距离和B到AO的距离,②熟练地运用锐角三角形函数的定义求出关系式,题目较好,但是一道比较容易出错的题目.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 (2011•峨眉山市二模)如图,在Rt△ABO中,OB=8,tan∠OBA=
(2011•峨眉山市二模)如图,在Rt△ABO中,OB=8,tan∠OBA=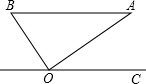
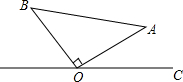 如图,在Rt△ABO中,直角边AO=BO=5.若点A到OC的距离为3,则点B到OC的距离为
如图,在Rt△ABO中,直角边AO=BO=5.若点A到OC的距离为3,则点B到OC的距离为 如图,在Rt△ABO中,∠OAB=90°,∠B=45°,OA=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1,则线段OA1的长与∠AOB1的度数分别为( )
如图,在Rt△ABO中,∠OAB=90°,∠B=45°,OA=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1,则线段OA1的长与∠AOB1的度数分别为( )