题目内容
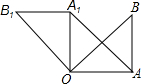如图，在Rt△ABO中，∠OAB=90°，∠B=45°，OA=6，将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1，则线段OA1的长与∠AOB1的度数分别为（ ）分析：△OAB是等腰直角三角形，△OAB绕点O沿逆时针方向旋转90°得到△OA1B1，则△OAB≌△OA1B1，根据全等三角形的性质即可求解．
解答：解：∵，△OAB绕点O沿逆时针方向旋转90°得到△OA1B1，
∴△OAB≌△OA1B1，
∴OA1=OA=6；
∵△OAB是等腰直角三角形，
∴∠A1OB=45°
∴∠AOB1=∠BOB1+∠BOA=90+45=135°．
故选：C．
∴△OAB≌△OA1B1，
∴OA1=OA=6；
∵△OAB是等腰直角三角形，
∴∠A1OB=45°
∴∠AOB1=∠BOB1+∠BOA=90+45=135°．
故选：C．
点评：本题主要考查了旋转的性质，图形旋转前后的两个图形全等，正确确定旋转角是解题关键．
练习册系列答案
相关题目
（2011•峨眉山市二模）如图，在Rt△ABO中，OB=8，tan∠OBA=
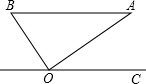
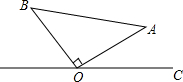如图，在Rt△ABO中，直角边AO=BO=5．若点A到OC的距离为3，则点B到OC的距离为
.若以O为坐标原点，OA所在直线为
轴，建立如图所示的平面直角坐标系，点C在
经过点A、B、C .