题目内容
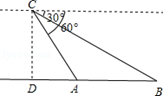
【题目】知识链接:将两个含![]() 角的全等三角尺放在一起, 让两个
角的全等三角尺放在一起, 让两个![]() 角合在一起成
角合在一起成![]() ,经过拼凑、观察、思考,探究出结论“直角三角形中,
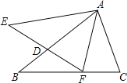
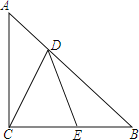
,经过拼凑、观察、思考,探究出结论“直角三角形中,![]() 角所对的直角边等于斜边的一半”.如图,等边三角形
角所对的直角边等于斜边的一半”.如图,等边三角形![]() 的边长为
的边长为![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 向
向![]() 运动,点
运动,点![]() 从
从![]() 出发沿
出发沿![]() 的延长线
的延长线![]() 向右运动,已知点
向右运动,已知点![]() 都以每秒
都以每秒![]() 的速度同时开始运动,运动过程中
的速度同时开始运动,运动过程中![]() 与
与![]() 相交于点
相交于点![]() ,设运动时间为
,设运动时间为![]() 秒.
秒.
![]() 请直接写出
请直接写出![]() 长. (用
长. (用![]() 的代数式表示)
的代数式表示)
![]() 当
当![]() 为直角三角形时,运动时间为几秒? .
为直角三角形时,运动时间为几秒? .
![]() 求证:在运动过程中,点
求证:在运动过程中,点![]() 始终为线段
始终为线段![]() 的中点.
的中点.
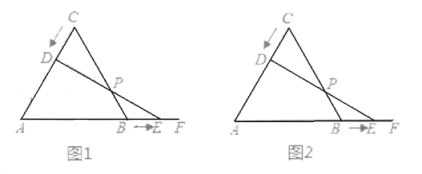
【答案】(1)AD=4-0.5x;(2)![]() 秒;(3)见解析
秒;(3)见解析
【解析】
(1)根据题意得到CD=0.5x,结合图形求出AD;
(2)设x秒时,△ADE为直角三角形,则BE=0.5x,AD=4-0.5x,AE=4+0.5x,根据30°的直角边等于斜边的一般建立方程求出其解即可;
(3)作DG∥AB交BC于点G,证明△DGP≌△EBP,得出PD=PE即可.
解:(1)由题意得,CD=0.5x,
则AD=4-0.5x;
(2)∵△ABC是等边三角形,
∴AB=BC=AC=4cm,∠A=∠ABC=∠C=60°.
设x秒时,△ADE为直角三角形,
∴∠ADE=90°,BE=0.5x,AD=4-0.5x,AE=4+0.5x,
∴∠AED=30°,
∴AE=2AD,
∴4+0.5x=2(4-0.5x),
∴x=![]() ;
;
答:运动![]() 秒后,△ADE为直角三角形;
秒后,△ADE为直角三角形;
(3)如图2,作DG∥AB交BC于点G,

∴∠GDP=∠BEP,∠DGP=∠EBP,∠CDG=∠A=60°,∠CGD=∠ABC=60°,
∴∠C=∠CDG=∠CGD,
∴△CDG是等边三角形,
∴DG=DC,
∵DC=BE,
∴DG=BE.
在△DGP和△EBP中,
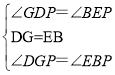 ,
,
∴△DGP≌△EBP(ASA),
∴DP=PE,
∴在运动过程中,点P始终为线段DE的中点.

 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
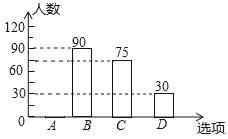
激活思维优加课堂系列答案【题目】某校决定在4月7日开展“世界无烟日”宣传活动,活动有A社区板报、B集会演讲、C喇叭广播、D发宣传画四种宣传方式.学校围绕“你最喜欢的宣传方式是什么?”,在全校学生中进行随机抽样调查四个选项中必选且只选一项,根据调查统计结果,绘制了两种不完整的统计图表.
选项 | 方式 | 百分比 |
A | 社区板报 | m |
B | 集会演讲 | 30% |
C | 喇叭广播 | 25% |
D | 发宣传画 | 10% |
请结合统计图表,回答下列问题:
(1)本次抽查的学生共 人,m= ,并将条形统计图补充完整;
(2)若该校学生有900人,请你估计该校喜欢“集会演讲”这项宣传方式的学生约有多少人?
(3)学校采用抽签方式让每班在A、B、C、D四种宣传方式中随机抽取两种进行展示.请用树状图或列表法求某班所抽到的两种方式恰好是“集会演讲”和“喇叭广播”的概率.