题目内容
 25、已知;如图,AB是半圆O的直径,弦CD∥AB,直线CM、DN分别切半圆于点C、D,且分别和直线AB相交于点M、N.
25、已知;如图,AB是半圆O的直径,弦CD∥AB,直线CM、DN分别切半圆于点C、D,且分别和直线AB相交于点M、N.(1)求证;MO=NO;
(2)设∠M=30°,求证:MN=4CD.
分析:(1)连接CO、DO,则有OC=OD,且OC⊥CM,OD⊥DN,易证△MCO≌△NDO,故MO=NO;
(2)先证△OCD为等边三角形,CD=OC,Rt△MCO中,OC=OA,∠M=30°,故MA=AO=OC,同理可得NB=OB=OC,故MN=4CD.
(2)先证△OCD为等边三角形,CD=OC,Rt△MCO中,OC=OA,∠M=30°,故MA=AO=OC,同理可得NB=OB=OC,故MN=4CD.
解答: 解:(1)证明:连接CO、DO,
解:(1)证明:连接CO、DO,
则有OC=OD,且OC⊥CM,OD⊥DN,
∴∠ODC=∠OCD,∠MCO=∠NDO=90°.
又∵CD∥AB,
∴∠OCD=∠MOC,∠ODC=∠NOD.
∴△MCO≌△NDO.
∴MO=NO.
(2)∵∠M=30°,
∴∠AOC=60°.
又∵AB∥CD,
∴∠OCD=60°.
∴△OCD为等边三角形.
∴CD=OC.
又∵Rt△MCO中,OC=OA,∠M=30°,
∴MA=AO=OC.
同理可得NB=OB=OC,
∴MN=4CD.
 解:(1)证明:连接CO、DO,
解:(1)证明:连接CO、DO,则有OC=OD,且OC⊥CM,OD⊥DN,
∴∠ODC=∠OCD,∠MCO=∠NDO=90°.
又∵CD∥AB,
∴∠OCD=∠MOC,∠ODC=∠NOD.
∴△MCO≌△NDO.
∴MO=NO.
(2)∵∠M=30°,
∴∠AOC=60°.
又∵AB∥CD,
∴∠OCD=60°.
∴△OCD为等边三角形.
∴CD=OC.
又∵Rt△MCO中,OC=OA,∠M=30°,
∴MA=AO=OC.
同理可得NB=OB=OC,
∴MN=4CD.
点评:本题综合考查了圆周角定理,全等三角形的判定,等边三角形的性质及平行线的性质.解答这类题一些学生不会综合运用所学知识解答问题,不知从何处入手造成错解.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
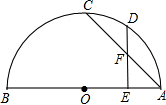 已知:如图,AB为⊙O的直径,C、D是半圆弧上的两点,E是AB上除O外的一点,AC与DE相交于F.①
已知:如图,AB为⊙O的直径,C、D是半圆弧上的两点,E是AB上除O外的一点,AC与DE相交于F.①
 =-
=- ,②DE⊥AB,③AF=DF.
,②DE⊥AB,③AF=DF.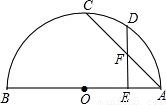
 ,②DE⊥AB,③AF=DF.
,②DE⊥AB,③AF=DF.
 ,②DE⊥AB,③AF=DF.
,②DE⊥AB,③AF=DF.