题目内容
已知：如图，在△DBC中，BC=DC,过点C作CE⊥DC交DB的延长线于点E，过点C作AC⊥BC且AC=EC，连结AB．
求证：AB=ED.
求证：AB=ED.
证明见解析.
试题分析：根据垂直的定义可得∠DCE=∠BAC=90°，然后利用“边角边”证明△ABC和△EDC全等，再根据全等三角形对应边相等证明即可．
试题解析：∵CE⊥DC，AC⊥BC，∴∠DCE=∠BAC=90°.
在△ABC和△EDC中，
，
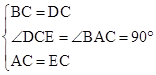练习册系列答案
相关题目
试题分析：根据垂直的定义可得∠DCE=∠BAC=90°，然后利用“边角边”证明△ABC和△EDC全等，再根据全等三角形对应边相等证明即可．
试题解析：∵CE⊥DC，AC⊥BC，∴∠DCE=∠BAC=90°.
在△ABC和△EDC中，
，
=k．
，则AB的长为（ ）
