题目内容
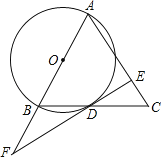
【题目】如图,在△ABC中,AB=AC,以AB为直径作⊙O交BC于点D,过点D作⊙O的切线DE交AC于点E,交AB延长线于点F.
(1)求证:DE⊥AC;
(2)若AB=10,BF=![]() ,求AE的长.
,求AE的长.
【答案】(1)见解析;(2)AE=8.
【解析】
(1)连接OD、AD,由AB=AC且∠ADB=90°知D是BC的中点,由O是AB中点知OD∥AC,根据OD⊥DE进一步求证即可;
(2)通过证明△ODF∽△AEF,可得![]() ,据此进一步求AE的长即可.
,据此进一步求AE的长即可.
(1)连接OD、AD,
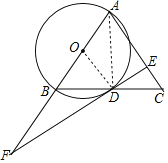
∵DE切⊙O于点D,
∴OD⊥DE,
∵AB是直径,
∴∠ADB=90°,
∵AB=AC,
∴D是BC的中点,
又∵O是AB中点,
∴OD∥AC,
∵OD⊥DE,
∴DE⊥AC;
(2)∵AB=10,
∴OA=OB=OD=5,
∴OF=BO+BF=![]() ,AF=BF+AB=
,AF=BF+AB=![]() ,
,
由(1)得OD∥AC,
∴∠ODF=∠AEF,∠F=∠F,
∴△ODF∽△AEF,
∴![]() ,
,
∴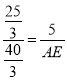 ,
,
∴AE=8.

【题目】为了丰富同学们的知识,拓展阅读视野,学习图书馆购买了一些科技、文学、历史等书籍,进行组合搭配成![]() 、
、![]() 、
、![]() 三种套型书籍,发放给各班级的图书角供同学们阅读,已知各套型的规格与价格如下表:
三种套型书籍,发放给各班级的图书角供同学们阅读,已知各套型的规格与价格如下表:
|
|
| |
规格(本/套) | 12 | 9 | 7 |
价格(元/套) | 200 | 150 | 120 |
(1)已知搭配![]() 、
、![]() 两种套型书籍共15套,需购买书籍的花费是2120元,问
两种套型书籍共15套,需购买书籍的花费是2120元,问![]() 、
、![]() 两种套型各多少套?
两种套型各多少套?
(2)若图书馆用来搭配的书籍共有2100本,现将其搭配成![]() 、
、![]() 两种套型书籍,这两种套型的总价为30750元,求搭配后剩余多少本书?
两种套型书籍,这两种套型的总价为30750元,求搭配后剩余多少本书?
(3)若图书馆用来搭配的书籍共有122本,现将其搭配成![]() 、
、![]() 、
、![]() 三种套型书籍共13套,且没有剩余,请求出所有搭配的方案.
三种套型书籍共13套,且没有剩余,请求出所有搭配的方案.
【题目】某校九年级共有400名学生,男女生人数大致相同,调查小组为调查学生的体质健康水平,开展了一次调查研究,将下面的过程补全.
收集数据:
调查小组选取40名学生的体质健康测试成绩作为样本,数据如下:
77 83 80 64 86 90 75 92 83 81
85 86 88 62 65 86 97 96 82 73
86 84 89 86 92 73 57 77 87 82
91 81 86 71 53 72 90 76 68 78
整理、描述数据:
2018年九年级部分学生学生的体质健康测试成绩统计表
成绩 | 50≤x<55 | 55≤x<60 | 60≤x<65 | 65≤x<70 | 70≤x<75 |
人数 | 1 | 1 | 2 | 2 | 4 |
成绩 | 75≤x<80 | 80≤x<85 | 85≤x<90 | 90≤x<95 | 95≤x<100 |
人数 | 5 | a | b | 5 | 2 |
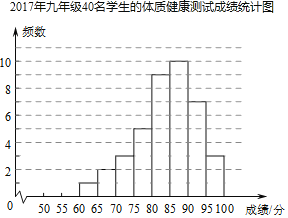
分析数据:
(1)写出表中的a、b的值;
(2)分析上面的统计图、表,你认为学生的体重健康测试成绩是2017年还是2018年的好?说明你的理由.(至少写出两条).
(3)体育老师根据2018年的统计数据,安排80分以下的学生进行体育锻炼,那么全年级大约有多少人参加?
【题目】已知二次函数y=x2﹣2x﹣1.
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … |
|
|
|
|
| … |
(1)请在表内的空格中填入适当的数;
(2)根据列表,请在所给的平面直角坐标系中画出y=x2﹣2x﹣1的图象;
(3)当x在什么范围内时,y随x增大而减小;