题目内容
【题目】顺次连接四边形各边中点,所得的图形是__________。顺次连接对角线______________的四边形的各边中点所得的图形是矩形。顺次连接对角线_________的四边形的各边中点所得的四边形是菱形。顺次连接对角线_________的四边形的各边中点所得的四边形是正方形。
【答案】平行四边形 互相垂直 相等 互相垂直且相等
【解析】试题解析:顺次连接四边形各边中点,所得的图形是平行四边形;
(如图)

根据中位线定理可得: ![]() 且GF∥BD,
且GF∥BD, ![]() 且EH∥BD,
且EH∥BD,
∴EH=FG,EH∥FG,
∴四边形EFGH是平行四边形;
顺次连接对角线互相垂直的四边形的各边中点所得的图形是矩形;
如图:

∵E、F.G、H分别为各边中点,
∴EF∥GH∥DB, ![]() ,
, ![]()
EH∥FG∥BD,
∵DB⊥AC,
∴EF⊥EH,
∴四边形EFGH是矩形;
顺次连接对角线相等的四边形的各边中点所得的四边形是菱形;
如图,
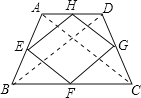
∵AC=BD,E. F.G、H分别是线段AB、BC、CD、AD的中点
∴EH、FG分别是△ABD、△BCD的中位线,EF、HG分别是△ACD、△ABC的中位线
根据三角形的中位线的性质,
∴![]()
∵AC=BD,
∴EH=FG=FG=EF,
∴四边形EFGH是菱形;
根据正方形的判别方法知,对角线互相平分,互相垂直且相等的四边形是正方形.
故答案为:平行四边形、互相垂直、相等、互相垂直且相等.

 阅读快车系列答案
阅读快车系列答案【题目】某商场销售A,B两种品牌的教学设备,这两种教学设备的进价和售价如表所示
A | B | |
进价(万元/套) | 1.5 | 1.2 |
售价(万元/套) | 1.65 | 1.4 |
该商场计划购进两种教学设备若干套,共需66万元,全部销售后可获毛利润9万元.
(1)该商场计划购进A,B两种品牌的教学设备各多少套?
(2)通过市场调研,该商场决定在原计划的基础上,减少A种设备的购进数量,增加B种设备的购进数量,已知B种设备增加的数量是A种设备减少的数量的1.5倍.若用于购进这两种教学设备的总资金不超过69万元,问A种设备购进数量至多减少多少套?