题目内容
若关于x的二次函数y=x2-2mx+1的图象与端点在(-1,1)和(3,4)的线段只有一个交点,则m的值可能是
- A.

- B.
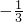
- C.

- D.

A
分析:由于二次函数y=x2-2mx+1的图象开口向上且过(0,1),与端点在(-1,1)和(3,4)的线段只有一个交点,则与过(-1,1)和(3,4)直线有两个交点,求出直线解析式,进而得出x2-(2m+ )x-
)x- =0在[-1,3]上有且仅有一个解,则f(x)=x2-(2m+
=0在[-1,3]上有且仅有一个解,则f(x)=x2-(2m+ )x-
)x- ,可以得出:f(-1)×f(3)≤0,然后解关于m的不等式.
,可以得出:f(-1)×f(3)≤0,然后解关于m的不等式.
解答:∵设直线AB过点(-1,1)和(3,4),
∴设直线AB的解析式为:y=kx+b,将两点代入解析式得:
 ,
,
解得:
故AB直线方程为:y= x+
x+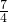 ,
,
根据y= x+
x+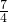 与y=x2-2mx+1在x=[-1,3]上有且仅有一个交点,
与y=x2-2mx+1在x=[-1,3]上有且仅有一个交点,
即 x+
x+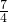 =x2-2mx+1,
=x2-2mx+1,
故x2-(2m+ )x-
)x- =0在[-1,3]上有且仅有一个解,
=0在[-1,3]上有且仅有一个解,
f(x)=x2-(2m+ )x-
)x- ,可以得出:f(-1)×f(3)≤0
,可以得出:f(-1)×f(3)≤0
则[1+2m]×[9-3(2m+ )-
)- ]≤0
]≤0
(1+2m)(-6m+6)≤0
即(1+2m)(6m-6)≥0,
即 或
或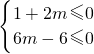 ,
,
解得:m≥1或m≤- .
.
只有 在这个范围内,
在这个范围内,
故选:A.
点评:本题考查了二次函数的性质,利用函数的单调性求函数f(x)=x2-(2m+ )x-
)x- 在区间[-1,3]上的值域是解决此题的关键.
在区间[-1,3]上的值域是解决此题的关键.
分析:由于二次函数y=x2-2mx+1的图象开口向上且过(0,1),与端点在(-1,1)和(3,4)的线段只有一个交点,则与过(-1,1)和(3,4)直线有两个交点,求出直线解析式,进而得出x2-(2m+
 )x-
)x- =0在[-1,3]上有且仅有一个解,则f(x)=x2-(2m+
=0在[-1,3]上有且仅有一个解,则f(x)=x2-(2m+ )x-
)x- ,可以得出:f(-1)×f(3)≤0,然后解关于m的不等式.
,可以得出:f(-1)×f(3)≤0,然后解关于m的不等式.解答:∵设直线AB过点(-1,1)和(3,4),
∴设直线AB的解析式为:y=kx+b,将两点代入解析式得:
 ,
,解得:

故AB直线方程为:y=
 x+
x+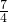 ,
,根据y=
 x+
x+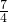 与y=x2-2mx+1在x=[-1,3]上有且仅有一个交点,
与y=x2-2mx+1在x=[-1,3]上有且仅有一个交点,即
 x+
x+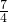 =x2-2mx+1,
=x2-2mx+1,故x2-(2m+
 )x-
)x- =0在[-1,3]上有且仅有一个解,
=0在[-1,3]上有且仅有一个解,f(x)=x2-(2m+
 )x-
)x- ,可以得出:f(-1)×f(3)≤0
,可以得出:f(-1)×f(3)≤0则[1+2m]×[9-3(2m+
 )-
)- ]≤0
]≤0(1+2m)(-6m+6)≤0
即(1+2m)(6m-6)≥0,
即
 或
或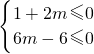 ,
,解得:m≥1或m≤-
 .
.只有
 在这个范围内,
在这个范围内,故选:A.
点评:本题考查了二次函数的性质,利用函数的单调性求函数f(x)=x2-(2m+
 )x-
)x- 在区间[-1,3]上的值域是解决此题的关键.
在区间[-1,3]上的值域是解决此题的关键. 
练习册系列答案
相关题目
 已知关于x 的一元二次方程(m+2)x2-2x-1=0.
已知关于x 的一元二次方程(m+2)x2-2x-1=0.