题目内容
【题目】某零件制造车间有工人20名，已知每名工人每天可制造甲种零件6个或乙种零件5个，且每制造一个甲种零件，可获利润150元，每制造一个乙种零件可获利润260元，在这20名工人中，车间每天安排
名工人制造甲种零件，其余工人制造乙种零件，且生产乙种零件的个数不超过甲种零件个数的一半．
（1）请写出此车间每天所获利润
（元）与（人）之间的函数关系式；
（2）求自变量的取值范围；
（3）怎样安排生产每天获得的利润最大，最大利润是多少？
【答案】（1）
；（2）
（3）安排13人生产甲种零件，安排7人生产乙种零件，所获利润最大，最大利润为20800元．
【解析】
（1）整个车间所获利润=甲种零件所获总利润+乙种零件所获总利润；
（2）根据零件零件个数均为非负整数以及乙种零件的个数不超过甲种零件个数的一半可得自变量的取值范围；
（3）根据（1）得到的函数关系式可得当x取最小整数值时所获利润最大．
解答
解：（1）此车间每天所获利润
（元）与
（人）之间的函数关系式是
．
（2）由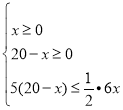
解得
因为为整数，所以
（3）
随的增大而减小，
当
时，
．
即安排13人生产甲种零件，安排7人生产乙种零件，所获利润最大，最大利润为20800元．
【题目】下表是小明记录的他家上月前几日汽车里程显示的数据.
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
里程表显示数据（公里） | 1121 | 1147 | 1215 | 1241 | 1262 | 1289 | 1373 |
(1)求小明家平均每天汽车行驶多少公里?
(2)小明家汽车耗油量为:每百公里耗油8升，加油站汽油价格为8元/升，上月按30天计算.求小明家要支付多少燃油费?
【题目】十八世纪瑞士数学家欧拉证明了简单多面体中项点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式，被称为欧拉公式。请你观察下列儿种简单多面体模型，解答下列问题:
(1)根据上面多面体模型，完成表格中的空格:
多面体 | 项点数(V) | 面数(F) | 棱数(F) |
四面体 | |||
长方体 | |||
正八面体 | |||
正十二面体 |
你发现项点数(V)、面数(F)、棱数(F)之间存在的关系式是__________________________.
（2）一个多面体的面数比顶点数小8，且有30条棱，则这多面体的顶点数是 20；
（3）某个玻璃饰品的外形是简单多面体，它的外表是由三角形和八边形两种多边形拼接而成，且有48个顶点，每个顶点处都有3条棱，设该多面体表面三角形的个数为x个，八边形的个数为y个，求x+y的值．
