��Ŀ����
����Ŀ�����壺��ƽ��ֱ������ϵxOy�У�ֱ��y��a��x��m��+k��Ϊ������y��a��x��m��2+k�Ĺ���ֱ�ߣ�
��1����������y��x2+6x��1�Ĺ���ֱ�ߣ�
��2����֪������y��ax2+bx+c�����Ĺ���ֱ��y��2x+3������y����ͬһ�㣬�����������ߵı���ʽ��
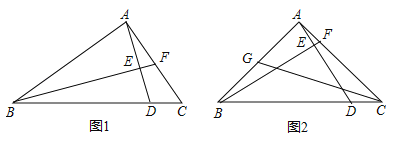
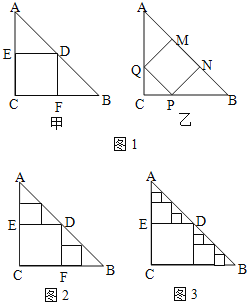
��3����ͼ�������ڵ�һ����������y����a��x��1��2+4a�����Ĺ���ֱ�߽��ڵ�A��B����A�ڵ�B����ࣩ����x�Ḻ���ύ�ڵ�C������AC��BC������ABCΪֱ��������ʱ����a��ֵ��

���𰸡���1��y��x+3��10��x��7����2��y��2x2+3��y��2��x+1��2+1����3��a=1��a=![]() .
.
��������
��1���Ƚ������ߵĽ���ʽ��Ϊ����ʽ��Ȼ����ݹ���ֱ�ߵĶ��弴�ɵó��𰸣�
��2��������ɵ�a=2��c=3���������ߵĶ���ʽΪy=2��x-m��2+k���ɵ�![]() ������m��k��ֵ�����������������ߵı���ʽ��
������m��k��ֵ�����������������ߵı���ʽ��
��3��������ɵ�A��1��4a����B��2��3a����C��-1��0��������AB2=1+a2��BC2=9+9a2��AC2=4+16a2����BC��ACΪб������������ۣ����ݹ��ɶ�������a��ֵ��
�⣺��1����y��x2+6x��1����x+3��2��10��
�����ֱ��Ϊy��x+3��10��x��7��
��2����������y��ax2+bx+c�����Ĺ���ֱ��y��2x+3������y����ͬһ�㣬
��a��2��c��3��
���������ߵĶ���ʽΪy��2��x��m��2+k��
�������ֱ��Ϊy��2��x��m��+k��2x��2m+k��
��![]() ��
��
���![]() ��
��![]() ��
��
�������߽���ʽΪy��2x2+3��y��2��x+1��2+1��
��3�������⣺A��1��4a��B��2��3a��C����1��0����
��AB2��1+a2��BC2��9+9a2��AC2��4+16a2��
��ȻAB2��BC2 ��AB2��AC2����AB���ܳ�Ϊ��ABC��б�ߣ�
��AB2+BC2��AC2ʱ��1+a2+9+9a2��4+16a2���a����1��
��AB2+AC2��BC2ʱ��1+a2+4+16a2��9+9a2���a=![]() ��
��
�������ߵĶ����ڵ�һ���ޣ�
��a��0����a=1��a=![]() .
.

 ��������ܸ�ϰϵ�д�
��������ܸ�ϰϵ�д�