题目内容
【题目】如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数![]() 的图象交于A、B两点,与x轴交于点C;点A在第一象限,点B的坐标为(﹣6,n);E为x轴正半轴上一点,且tan∠AOE=
的图象交于A、B两点,与x轴交于点C;点A在第一象限,点B的坐标为(﹣6,n);E为x轴正半轴上一点,且tan∠AOE=![]() .
.
(1)求点A的坐标;
(2)求一次函数的表达式;
(3)求△AOB的面积.
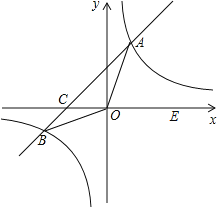
【答案】(1)A(3,4);(2)y=![]() x+2;(3)9.
x+2;(3)9.
【解析】
(1)过A作AH⊥x轴于点H,根据tan∠AOE=![]() ,设OH=3k,AH=4k,即A的坐标为(3k,4k),代入反比例函数解析式即可求出A点的坐标;
,设OH=3k,AH=4k,即A的坐标为(3k,4k),代入反比例函数解析式即可求出A点的坐标;
(2)求出B点的坐标,把A、B的坐标代入y=kx+b即可求出k、b的值,即可求出答案;
(3)求出OC,根据三角形面积公式求出即可.
解:(1)过A作AH⊥x轴于点H,
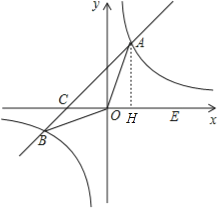
在Rt△AOH中,∵tan∠AOE=![]() ,
,
∴设OH=3k,AH=4k,
即A的坐标为(3k,4k),其中k>0,
∵A在![]() 图象上,
图象上,
∴![]() ,
,
解得:k=1(负数舍去),
∴A的坐标为(3,4);
(2)∵点B(﹣6,n)在![]() 的图象上,
的图象上,
∴代入得:n=﹣2,
即B的坐标为(﹣6,﹣2),
把A、B的坐标代入y=kx+b(k≠0)得:![]() ,
,
解得:k=![]() ,b=2,
,b=2,
∴一次函数的表达式是y=![]() x+2;
x+2;
(3)在y=![]() x+2中令y=0,则x=﹣3,
x+2中令y=0,则x=﹣3,
即C(﹣3,0),
所以S△AOB=S△AOC+S△BOC=![]() ×|﹣3|×4+
×|﹣3|×4+![]() ×|﹣3|×|﹣2|=9,
×|﹣3|×|﹣2|=9,
即△AOB的面积是9.

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案【题目】小东根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
(1)函数![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x | … |
|
|
| 0 |
| 1 |
| 2 |
| 3 | 4 | … |
y | … |
|
|
| 2 |
| 4 |
| 2 |
|
| m | … |
表中m的值为________________;
(3)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点. 根据描出的点,画出函数![]() 的大致图象;
的大致图象;
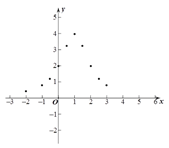
(4)结合函数图象,请写出函数![]() 的一条性质:______________________.
的一条性质:______________________.
(5)解决问题:如果函数![]() 与直线y=a的交点有2个,那么a的取值范围是______________ .
与直线y=a的交点有2个,那么a的取值范围是______________ .