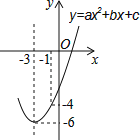题目内容
【题目】某水果批发商经营甲、乙两种水果,根据以往经验和市场行情,预计夏季某一段时间内,甲种水果的销售利润![]() (万元)与进货量x(吨)近似满足函数关系
(万元)与进货量x(吨)近似满足函数关系![]() ,乙种水果的销售利润
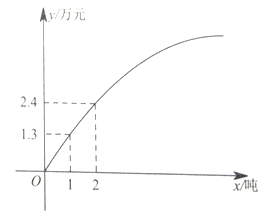
,乙种水果的销售利润![]() (万元)与进货量x(吨)之间的函数关系如图所示.
(万元)与进货量x(吨)之间的函数关系如图所示.
(1)求![]() (万元)与x(吨)之间的函数关系式;
(万元)与x(吨)之间的函数关系式;
(2)如果该批发商准备进甲、乙两种水果共10吨,设乙种水果的进货量为t吨,请你求出这两种水果所获得的销售利润总和W(万元)与t(吨)之间的函数关系式.并求出这两种水果各进多少吨时获得的销售利润总和最大,最大利润是多少?
【答案】(1)![]() ;(2)甲、乙两种水果的进货量分别为4吨和6吨时,获得的销售利润总和最大,最大利润是5.6万元.
;(2)甲、乙两种水果的进货量分别为4吨和6吨时,获得的销售利润总和最大,最大利润是5.6万元.
【解析】
(1)根据题意列出二元一次方程组,求出a、b的值即可求出函数关系式的解.
(2)由题意可得![]() ,用配方法化简函数关系式即可求出w的最大值.
,用配方法化简函数关系式即可求出w的最大值.
(1)根据图象,可设![]() (其中
(其中![]() ,a,b为常数),
,a,b为常数),
由题意,得解得![]() 解得
解得![]()
∴![]() .
.
(2)∵乙种水果的进货量为t吨,则甲种水果的进货量为![]() 吨,
吨,
由题意,得![]() .
.
将函数配方为顶点式,得![]() .
.
∵![]() ,∴抛物线开口向下.
,∴抛物线开口向下.
∵![]() ,∴
,∴![]() 时,W有最大值为5.6.
时,W有最大值为5.6.
∴![]() (吨).
(吨).
答:甲、乙两种水果的进货量分别为4吨和6吨时,获得的销售利润总和最大,最大利润是5.6万元.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目