题目内容
若⊙O的半径为10,弦AB=12,弦CD=16,且AB∥CD,则两条弦间的距离为______.
分为两种情况:
①如图,
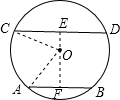
过O作EF⊥DC于E,交AB于F,连接OC、OA,
∵AB∥CD,
∴EF⊥AB,
由垂径定理得:CE=
CD=
×16=8,AF=
AB=
×12=6,
在Rt△CEO中,由勾股定理得:OE=
=
=6,
同理OF=8,
∴EF=OE+OF=6+8=14;
②如图

EF=OF-OE=8-6=2;
故答案为:14或2.
①如图,

过O作EF⊥DC于E,交AB于F,连接OC、OA,
∵AB∥CD,
∴EF⊥AB,
由垂径定理得:CE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△CEO中,由勾股定理得:OE=
| OC2-CE2 |
| 102-82 |
同理OF=8,
∴EF=OE+OF=6+8=14;
②如图

EF=OF-OE=8-6=2;
故答案为:14或2.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目







