题目内容
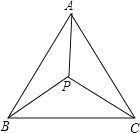
【题目】如图5,点P在正△ABC内一点,∠APB=125°, ∠BPC=100°,则以AP,BP,CP为边长的三角形各内角的度数为________.
【答案】40°,65°,75°
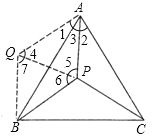
【解析】试题解析:将△APC绕点A顺时针旋转60°得△AQB,则△AQB≌△APC,
∴BQ=CP,AQ=AP,
∵∠1+∠3=60°,
∴△APQ是等边三角形,
∴QP=AP,
∴△QBP就是以AP,BP,CP三边为边的三角形.
∵∠APC=360°-∠APB-∠BPC=135°,
∴∠6=∠APB-∠5=65°,
∵∠AQB=∠APC=135°,
∴∠7=∠AQB-∠4=75°,
∴∠QBP=180°-∠6-∠7=40°,
∴以AP,BP,CP为边的三角形的三内角的度数分别为75°,65°,40°.

练习册系列答案
相关题目