题目内容
【题目】已知:Rt△ABC中,∠C=90°,AC=3,BC=4,P为AB上任意一点,PF⊥AC于F,PE⊥BC于E,则EF的最小值是_____.

【答案】2.4
【解析】
连接CP,利用勾股定理列式求出AB,判断出四边形CFPE是矩形,根据矩形的对角线相等可得EF=CP,再根据垂线段最短可得CP⊥AB时,线段EF的值最小,然后根据三角形的面积公式列出方程求解即可.
解:如图,连接CP,
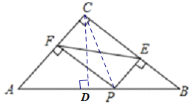
∵∠C=90°,AC=3,BC=4,
∴AB=![]() =5,
=5,
∵PE⊥AC,PF⊥BC,∠C=90°,
∴四边形CFPE是矩形,
∴EF=CP,
过C点作CD⊥AB,
由垂线段最短可得CP⊥AB时,即CP=CD时,线段EF的值最小,
此时,S△ABC=![]() BCAC=
BCAC=![]() ABCP,即
ABCP,即![]() ×4×3=
×4×3=![]() ×5CP,
×5CP,
解得CP=2.4.
故答案为:2.4.

练习册系列答案
相关题目