题目内容
将边长为8cm的正方形ABCD的四边沿直线l向右滚动(不滑动),当正方形滚动两周时,正方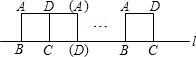 形的顶点A所经过的路线的长是
形的顶点A所经过的路线的长是分析:可先计算旋转周时,正方形的顶点A所经过的路线的长,可以看出是四段弧长,根据弧长公式计算即可.
解答:解:第一次旋转是以点C为圆心,AC为半径,旋转角度是90度,
所以弧长=
=4
π;
第二次旋转是以点D为圆心,AD为半径,角度是90度,
所以弧长=
=4π;
第三次旋转是以点A为圆心,所以没有路程;
第四次是以点B为圆心,AB为半径,角度是90度,
所以弧长=
=4π;
所以旋转一周的弧长共=4
π+8π.
所以正方形滚动两周正方形的顶点A所经过的路线的长是16π+8
π.
所以弧长=
90π×8
| ||
| 180 |
| 2 |
第二次旋转是以点D为圆心,AD为半径,角度是90度,
所以弧长=
| 90π×8 |
| 180 |
第三次旋转是以点A为圆心,所以没有路程;
第四次是以点B为圆心,AB为半径,角度是90度,
所以弧长=
| 90π×8 |
| 180 |
所以旋转一周的弧长共=4
| 2 |
所以正方形滚动两周正方形的顶点A所经过的路线的长是16π+8
| 2 |
点评:本题的关键是理清第一次旋转时的圆心及半径和圆心角的度数,然后利用弧长公式求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
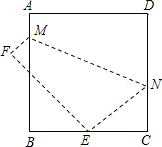 如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN,则线段CN长是( )
如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN,则线段CN长是( )| A、3cm | B、4cm | C、5cm | D、6cm |
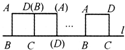 将边长为8cm的正方形ABCD的四边沿直线l向右滚动(不滑动),当正方形滚动两周时,正方形的顶点A所经过的路线的长是( )
将边长为8cm的正方形ABCD的四边沿直线l向右滚动(不滑动),当正方形滚动两周时,正方形的顶点A所经过的路线的长是( )A、(4
| ||
B、(8
| ||
C、(8
| ||
D、(4
|
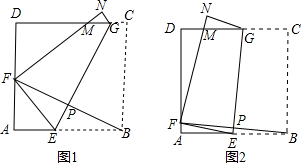
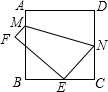 如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN,则线段CN的长是
如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN,则线段CN的长是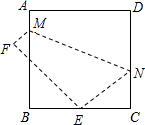 (2013•邓州市一模)如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN,则线段CN=
(2013•邓州市一模)如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN,则线段CN=