题目内容
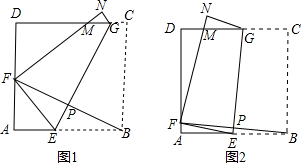
将边长为8cm的正方形纸片ABCD沿EG折叠(折痕EG分别与AB、DC交于点E、G),使点B落在AD边上的点 F处,FN与DC交于点M,连接BF与EG交于点P.(1)当点F与AD的中点重合时(如图1):
①△AEF的边AE=
(填“>”、“=”或“<”)
②求△FDM的周长.
(2)当点F在AD边上除点A、D外的任意位置时(如图2):
③试问第(1)题中线段EG与BF的大小关系是否发生变化?请证明你的结论;
④当点F在何位置时,四边形AEGD的面积S最大?最大值是多少?
分析:(1)①根据直角三角形勾股定理即可得出结论,②利用三角形相似对边比例关系计算出三角形各边长即可计算出结果,
(2)①根据题意,利用三角形全等即可证明结论,②根据勾股定理得出AE,然后利用全等三角形得出AF、AK,即可得出结果.
(2)①根据题意,利用三角形全等即可证明结论,②根据勾股定理得出AE,然后利用全等三角形得出AF、AK,即可得出结果.
解答: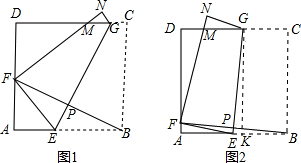 解:(1)①AE=3cm,EF=5cm;EG=BF,
解:(1)①AE=3cm,EF=5cm;EG=BF,
设AE=x,则EF=8-x,AF=4,∠A=90°,42+x2=(8-x)2,x=3,
∴AE=3cm,EF=5cm,EG=BF,
②解:如图1,∵∠MFE=90°,
∴∠DFM+∠AFE=90°,
又∵∠A=∠D=90°,∠AFE=∠DMF,
∴△AEF∽△DFM,
∴
=
=
,
又∵AE=3,AF=DF=4,EF=5,
∴
=
,FM=
,
=
,DM=
,
∴△FMD的周长=4+
+
=16;
(2)①EG=BF不会发生变化,
理由:证明:如图2,∵B、F关于GE对称,
∴BF⊥EG于P,过G作GK⊥AB于K,
∴∠FBE=∠KGE,
在正方形ABCD中,GK=BC=AB,∠A=∠EKG=90°,
∴△AFB≌△KEG(AAS),
∴EG=BF,
②如图2,设AF=x,EF=8-AE,x2+AE2=(8-AE)2,
∴AE=4-
x2,
∵△AFB≌△KEG,
∴AF=EK=x,AK=AE+EK=AF+AE=4-
x2+x,(10分)
S=
×8=0.5×8(AE+AK)=4×(4-
x2+4-
x2+x)=-
x2+4x+32,
S=-
(x-4)2+40,(0<x<8)
当x=4,即F与AD的中点重合时,S最大=40.(12分)
 解:(1)①AE=3cm,EF=5cm;EG=BF,
解:(1)①AE=3cm,EF=5cm;EG=BF,设AE=x,则EF=8-x,AF=4,∠A=90°,42+x2=(8-x)2,x=3,
∴AE=3cm,EF=5cm,EG=BF,
②解:如图1,∵∠MFE=90°,
∴∠DFM+∠AFE=90°,
又∵∠A=∠D=90°,∠AFE=∠DMF,
∴△AEF∽△DFM,
∴
| EF |
| FM |
| AE |
| DF |
| AF |
| DM |
又∵AE=3,AF=DF=4,EF=5,
∴
| 5 |
| FM |
| 3 |
| 4 |
| 20 |
| 3 |
| 3 |
| 4 |
| 4 |
| DM |
| 16 |
| 3 |
∴△FMD的周长=4+
| 20 |
| 3 |
| 16 |
| 3 |
(2)①EG=BF不会发生变化,
理由:证明:如图2,∵B、F关于GE对称,
∴BF⊥EG于P,过G作GK⊥AB于K,
∴∠FBE=∠KGE,
在正方形ABCD中,GK=BC=AB,∠A=∠EKG=90°,
∴△AFB≌△KEG(AAS),
∴EG=BF,
②如图2,设AF=x,EF=8-AE,x2+AE2=(8-AE)2,
∴AE=4-
| 1 |
| 16 |
∵△AFB≌△KEG,
∴AF=EK=x,AK=AE+EK=AF+AE=4-
| 1 |
| 16 |
S=
| AE+DG |
| 2 |
| 1 |
| 16 |
| 1 |
| 16 |
| 1 |
| 2 |
S=-
| 1 |
| 2 |
当x=4,即F与AD的中点重合时,S最大=40.(12分)
点评:本题主要考查旋转的性质以及全等三角形的判定和性质,需要注意的是:旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变,难度较大.

练习册系列答案
相关题目
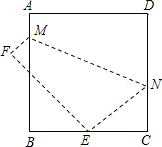 如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN,则线段CN长是( )
如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN,则线段CN长是( )| A、3cm | B、4cm | C、5cm | D、6cm |
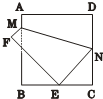 12、如图所示,将边长为8cm的正方形纸片ABCD折叠,使点D落在BC中点E处,点A落在F处,折痕为MN,则线段CN的长是( )
12、如图所示,将边长为8cm的正方形纸片ABCD折叠,使点D落在BC中点E处,点A落在F处,折痕为MN,则线段CN的长是( ) 如图,将边长为8cm的正方形纸片ABCD折叠,使点D落在BC边中点E处,点A落在点F处,折痕为MN,则线段CN的长度为
如图,将边长为8cm的正方形纸片ABCD折叠,使点D落在BC边中点E处,点A落在点F处,折痕为MN,则线段CN的长度为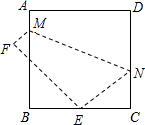 (2013•邓州市一模)如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN,则线段CN=
(2013•邓州市一模)如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN,则线段CN=