题目内容
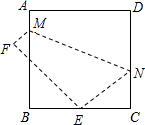 (2013•邓州市一模)如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN,则线段CN=
(2013•邓州市一模)如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN,则线段CN=3cm
3cm
,AM=1cm
1cm
.分析:分两步求解:
(1)在Rt△ECN中,利用勾股定理与折叠性质,求出CN的长度;
(2)过点M作MG⊥CD于点C,证明△MNG≌△DEC,得到GN=CE,从而求出DG,即AM的长度.
(1)在Rt△ECN中,利用勾股定理与折叠性质,求出CN的长度;
(2)过点M作MG⊥CD于点C,证明△MNG≌△DEC,得到GN=CE,从而求出DG,即AM的长度.
解答: 解:设CN=xcm,则DN=(8-x)cm.
解:设CN=xcm,则DN=(8-x)cm.
由折叠可知,EN=DN=(8-x)cm.
在Rt△ECN中,CE=4cm,CN=xcm,EN=(8-x)cm,
由勾股定理得:EN2=CN2+CE2,即(8-x)2=x2+42,
解得:x=3,
∴CN=3cm;
如图,过点M作MG⊥CD于点G,则由题意可知AM=DG,MG=BC=CD.
连接DE,交MG于点I.
由折叠可知,DE⊥MN,∴∠NMG+MIE=90°,
∵∠DIG+∠EDC=90°,∠MIE=∠DIG(对顶角相等),
∴∠NMG=∠EDC.
在△MNG与△DEC中,
∴△MNG≌△DEC(ASA).
∴GN=CE=4cm,
∴DG=CD-CN-GN=8-3-4=1cm.
∴AM=DG=1cm.
故答案为:3cm和1cm.
 解:设CN=xcm,则DN=(8-x)cm.
解:设CN=xcm,则DN=(8-x)cm.由折叠可知,EN=DN=(8-x)cm.
在Rt△ECN中,CE=4cm,CN=xcm,EN=(8-x)cm,
由勾股定理得:EN2=CN2+CE2,即(8-x)2=x2+42,
解得:x=3,
∴CN=3cm;
如图,过点M作MG⊥CD于点G,则由题意可知AM=DG,MG=BC=CD.
连接DE,交MG于点I.
由折叠可知,DE⊥MN,∴∠NMG+MIE=90°,
∵∠DIG+∠EDC=90°,∠MIE=∠DIG(对顶角相等),
∴∠NMG=∠EDC.
在△MNG与△DEC中,
|
∴△MNG≌△DEC(ASA).
∴GN=CE=4cm,
∴DG=CD-CN-GN=8-3-4=1cm.
∴AM=DG=1cm.
故答案为:3cm和1cm.
点评:考查了翻折问题,翻折问题关键是找准对应重合的量,哪些边、角是相等的.本题中DN=EN是解题关键,再利用勾股定理、全等三角形的知识就迎刃而解.

练习册系列答案
相关题目


 (2013•邓州市一模)如图,一个几何体是由大小相同的小正方体焊接而成,其主视图、俯视图、左视图都是“田”字形,则焊接该几何体所需小正方体的个数最少为
(2013•邓州市一模)如图,一个几何体是由大小相同的小正方体焊接而成,其主视图、俯视图、左视图都是“田”字形,则焊接该几何体所需小正方体的个数最少为 发沿线段CB方向以每秒3个单位长的速度向点B匀速运动;点P、Q同时出发,当点P与点D重合时停止运动,点Q也随之停止,设点P的运动时间为t秒.
发沿线段CB方向以每秒3个单位长的速度向点B匀速运动;点P、Q同时出发,当点P与点D重合时停止运动,点Q也随之停止,设点P的运动时间为t秒.