题目内容
(1)如图1,正方形ABCD的面积为2a,将正方形ABCD的对角线BD绕点B逆时针旋转90°至BE,以BD和BE为邻边作正方形BDFE,则此正方形BDFE的面积为(2)如图2所示,再将正方形BDFE的对角线BF绕点B逆时针旋转90°至BG,以BF和BG为邻边作正方形BFHG,则此正方形BFHG的面积为
(3)如果按着上述的过程作第三次旋转后,所得到的正方形的面积为
(4)在一块边长为10米的正方形空地内种植上草坪(如图3阴影部分所示),由于这块正方形空地的左边和前边都有许多空地,所以,就在它的左边和前边(按着图2所示的过程)连续两次对这块草坪扩大种植面积,最后如图3所示的整个区域内都种上草坪,那么此时的草坪面积是多少平方米?
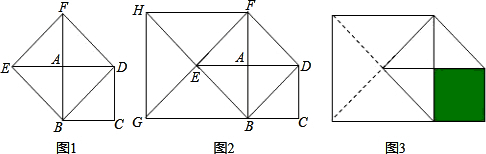
分析:(1)可求出边长AB,BD的长,继而可求出正方形BDFE的面积为4a.
(2)可求出边长GF,HG的长,继而可求出正方形BFHG的面积.
(3)观察(1),(2),可知其面积按2的倍数递增,可知下个正方形的面积为16a.
(4)根据规律可知图形的总面积为11a,a=50,易求出图形的总面积.
(2)可求出边长GF,HG的长,继而可求出正方形BFHG的面积.
(3)观察(1),(2),可知其面积按2的倍数递增,可知下个正方形的面积为16a.
(4)根据规律可知图形的总面积为11a,a=50,易求出图形的总面积.
解答:解:(1)已知正方形的面积为2a,则边长AB=
,
根据勾股定理可得BD=
,所以正方形BDFE的面积为4a;
(2)依题意得出GF=2
,则HG=
,
则正方形BFHG的面积为8a;
(3)根据规律可得下个正方形的面积为16a;
(4)依据上面的规律可知:图形的总面积为8a+a+2a=11a,
由题意得:2a=102,即a=50,
∴图形的总面积为11×50=550(平方米).
| ||
| 2 |
根据勾股定理可得BD=
| a |
(2)依题意得出GF=2
| a |
| 2a |
则正方形BFHG的面积为8a;
(3)根据规律可得下个正方形的面积为16a;
(4)依据上面的规律可知:图形的总面积为8a+a+2a=11a,
由题意得:2a=102,即a=50,
∴图形的总面积为11×50=550(平方米).
点评:本题综合考查了旋转的性质以及正方形的性质,考生要注意的是总结规律解答.

练习册系列答案
相关题目
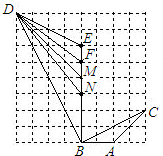 如图,在正方形网格上,与△ABC相似的三角形是( )
如图,在正方形网格上,与△ABC相似的三角形是( )| A、△NBD | B、△MBD | C、△EBD | D、△FBD |
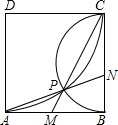 如图,在正方形ABCD内,以D点为圆心,AD长为半径的弧与以BC为直径的半圆交于点P,延长CP、AP交AB、BC于点M、N.若AB=2,则AP等于( )
如图,在正方形ABCD内,以D点为圆心,AD长为半径的弧与以BC为直径的半圆交于点P,延长CP、AP交AB、BC于点M、N.若AB=2,则AP等于( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
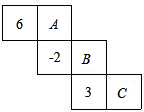 如图,是正方形的表面展形图,如果相对两个面数字之和相等,且A+B+C=14,则6A-2B+3C=
如图,是正方形的表面展形图,如果相对两个面数字之和相等,且A+B+C=14,则6A-2B+3C=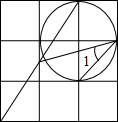 如图,在正方形网格图中,每个小正方形的边长均为 1,则∠1的正弦值是
如图,在正方形网格图中,每个小正方形的边长均为 1,则∠1的正弦值是 如图,在正方形ABCD中,E是BC上一点,且BC:EC=4:1,F是DC的中点.
如图,在正方形ABCD中,E是BC上一点,且BC:EC=4:1,F是DC的中点.