��Ŀ����
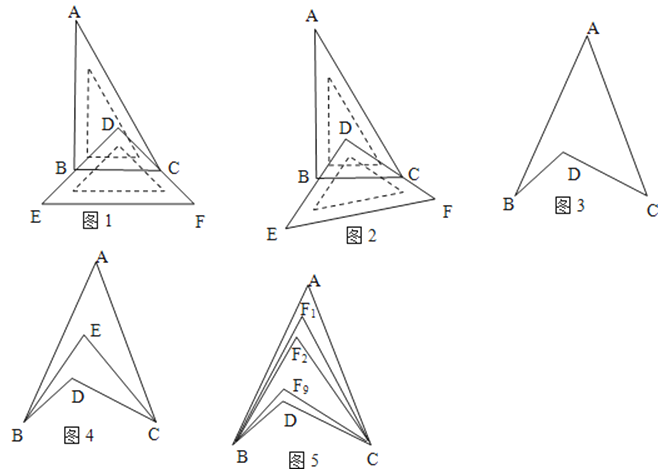
����Ŀ����ͼ�٣���һ��ֱ�����ǰ����ͬһ��ֱ��AB�ϣ����С�ONM=30�㣬��OCD=45�㣮
��1����ͼ���е����ǰ�OMN��BA�ķ���ƽ����ͼ�ڵ�λ�ã�MN��CD�ཻ�ڵ�E�����CEN�Ķ�����
��2����ͼ���е����ǰ�OMN�Ƶ�O����ʱ�뷽����ת����ͼ�ۣ�����CON=5��DOMʱ��MN��CD�ཻ�ڵ�E�������ж�MN��BC��λ�ù�ϵ�������CEN�Ķ���
��3����ͼ���е����ǰ�OMN�Ƶ�O��ÿ��5����ٶȰ���ʱ�뷽����תһ�ܣ�����ת�Ĺ����У����ǰ�MON�˶������ֱ��MNǡ����ֱ��CDƽ�У�
��4������ͼ��λ�õ��������ǰ�ͬʱ�Ƶ�O��ʱ����ת���ٶȷֱ�ÿ��20���ÿ��10�㣬������һ�����ǰ�ص���ʼλ��ʱ���������ǰ�ͬʱֹͣת����������������OC���ON���ഹֱ����ֱ��д���𰸣�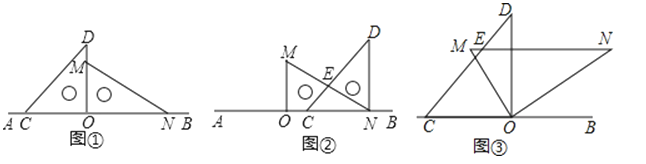
���𰸡��⣺��1���ڡ�CEN�У���CEN=180�㩁30�㩁45��=105�㣻
��2����ͼ�ڣ��ߡ�CON=5��DOM
��180�㩁��DOM=5��DOM��
���DOM=30��
�ߡ�OMN=60�㣬
��MN��OD��
��MN��BC��
���CEN=180�㩁��DCO=180�㩁45��=135�㣻
��3����ͼ�ۣ�MN��CDʱ����ת��Ϊ90�㩁��60�㩁45�㣩=75�㣬
��270�㩁��60�㩁45�㣩=255�㣬
���ԣ�t=75���5��=15�룬
��t=255���5��=51�룻
���ԣ�����ת�Ĺ����У����ǰ�MON�˶�15���51���ֱ��MNǡ����ֱ��CDƽ�У�
��4��MN��CDʱ����ת�ǵĽǶȲ���90�㣬
����90��£�20�㩁10�㣩=9�룬
�ʴ�Ϊ��9��
����������1�����������ε��ڽǺͶ�����ʽ���㼴�ɵý⣻
��2�����MN��OD��Ȼ�����ͬλ����ȣ���ֱ��ƽ���жϳ�MN��BC���ٸ�����ֱ��ƽ�У�ͬ���ڽǻ������
��3����������������ת�ǣ��ٸ���ʱ��=��ת�ǡ��ٶȼ��㼴�ɵý⣮
��4�������ת�ĽǶȲ�ٸ���ʱ��=��ת�Dz���ٶȲ���㼴�ɵý⣮