题目内容
已知一次函数y=kx+m和二次函数y=ax2+bx+c的图象相交于A（1，4）和B（-2，-5），并且二次函数y=ax2+bx+c的图象经过一次函数y=2x+3的图象与y轴的交点，试求一次函数与二次函数的解析式．
【答案】分析：将点A（1，4）和B（-2，-5）代入一次函数y=kx+m，利用待定系数法求一次函数的解析式；然后求出一次函数y=2x+3的图象与y轴的交点是（0，3），最后将A（1，4）、B（-2，-5）和
（0，3）代入二次函数y=ax2+bx+c，利用待定系数法求二次函数的解析式．
解答：解：∵一次函数y=kx+m和二次函数y=ax2+bx+c的图象相交于A（1，4）和B（-2，-5），
∴
，
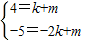解得，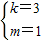
，
∴一次函数的解析式是：y=3x+1；
又∵一次函数y=2x+3的图象与y轴的交点是（0，3），
二次函数y=ax2+bx+c的图象经过一次函数y=2x+3的图象与y轴的交点，
∴
，
解得，
，
∴二次函数的解析式：y=-x2+2x+3．
点评：本题考查了待定系数法求一次函数、二次函数解析式．函数图象上的点都满足函数的解析式．
（0，3）代入二次函数y=ax2+bx+c，利用待定系数法求二次函数的解析式．
解答：解：∵一次函数y=kx+m和二次函数y=ax2+bx+c的图象相交于A（1，4）和B（-2，-5），
∴
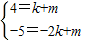，解得，
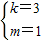，∴一次函数的解析式是：y=3x+1；
又∵一次函数y=2x+3的图象与y轴的交点是（0，3），
二次函数y=ax2+bx+c的图象经过一次函数y=2x+3的图象与y轴的交点，
∴
，解得，
，∴二次函数的解析式：y=-x2+2x+3．
点评：本题考查了待定系数法求一次函数、二次函数解析式．函数图象上的点都满足函数的解析式．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
已知一次函数y=kx+2的图象经过A（-1，1）．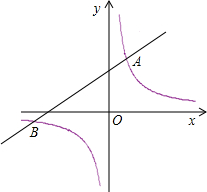
m≠0）的图象相交于点 A（1，3）、B（n，-1）两点．
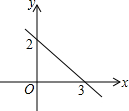已知一次函数y=kx+b的图象如图所示，指出k、b的符号，并求出k和b的值．