题目内容
【题目】要修建一个圆形喷水池，在池中心竖直安装一根水管，在水管的顶端安一个喷头，使喷出的抛物线形水柱在与水池中心的水平距离为1m处达到最高，高度为3m，水柱落地处离中心3m．
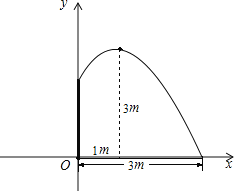
（1）在给定的坐标系中画出示意图；
（2）求出水管的长度．
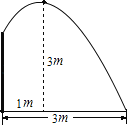
【答案】（1）详见解析；（2）水管长为2.25m．
【解析】
（1）以池中心为原点，竖直安装的水管为y轴，与水管垂直的为x轴建立直角坐标系；
（2）设抛物线的解析式为y＝a（x﹣1）2+3（0≤x≤3），将（3，0）代入求得a值，则x＝0时得的y值即为水管的长．
解：（1）建立以池中心为原点，竖直安装的水管为y轴，与水管垂直的为x轴建立直角坐标系；
（2）由于在距池中心的水平距离为1m时达到最高，高度为3m，
则设抛物线的解析式为：
y＝a（x﹣1）2+3（0≤x≤3），
代入（3，0）求得：a＝﹣
．
将a值代入得到抛物线的解析式为：
y＝﹣（x﹣1）2+3（0≤x≤3），
令x＝0，则y＝
＝2.25．
故水管长为2.25m．
练习册系列答案
相关题目
