题目内容
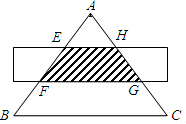如图，△ABC是等边三角形，被一平行于BC的矩形所截，AB被截成三等分，则图中阴影部分的面积是△ABC的面积的分析：根据题意，易证△AEH∽△AFG∽△ABC，利用相似比，可求出S△AEH、S△AFG面积比，再求出S△ABC．
解答：解：∵AB被截成三等分，
∴△AEH∽△AFG∽△ABC，
∴
=
，
=
，
∴S△AFG：S△ABC=4：9，
S△AEH：S△ABC=1：9，
∴S阴影部分的面积=
S△ABC-
S△ABC=
S△ABC．
故答案为
．
∴△AEH∽△AFG∽△ABC，
∴
| AE |
| AF |
| 1 |
| 2 |
| AE |
| AB |
| 1 |
| 3 |
∴S△AFG：S△ABC=4：9，
S△AEH：S△ABC=1：9，
∴S阴影部分的面积=
| 4 |
| 9 |
| 1 |
| 9 |
| 1 |
| 3 |
故答案为
| 1 |
| 3 |
点评：本题主要考查了利用三等分点求得各相似三角形的相似比，从而求出面积比计算阴影部分的面积，难度适中．
练习册系列答案
相关题目
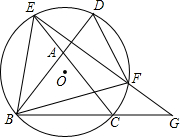∥AC，EF的延长线交BC的延长线于点G．
9、如图，△ABC是等边三角形，过AB边上一点D作BC的平行线交AC于E，则△ADE的三个内角
如图，△ABC是等边三角形，AB=4cm，则BC边上的高AD等于
如图，△ABC是等边三角形，D为BC边上的点，∠BAD=15°，将△ABD绕点A点逆时针方向旋转后到达△ACE的位置，那么旋转角的度数是
如图，△ABC是等边三角形，CE是外角平分线，点D在AC上，连结BD并延长与CE交于点E．