题目内容
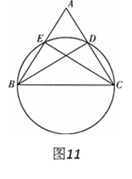
如图11,△ABC的两个顶点B、C在圆上,顶点A在圆外,AB、AC分别交圆于E、D两点,连结EC、BD.
(1)求证:△ABD∽△ACE;
(2)若ΔBEC与ΔBDC的面积相等,试判定△ABC的形状.

(1)证明:因![]() 为弧ED所对的圆周角相等,所以∠EBD=∠ECD, 又因为∠A=∠A,所以△
为弧ED所对的圆周角相等,所以∠EBD=∠ECD, 又因为∠A=∠A,所以△![]() ABD∽ΔACE. ………………………5分
ABD∽ΔACE. ………………………5分
(2)法1:因为S△BEC=S△BCD,
 S△ACE=S△ABC-S△B
S△ACE=S△ABC-S△B![]() EC,S△ABD=S△ABC一S△BCD, 所以S△ACE=S△ABD,
EC,S△ABD=S△ABC一S△BCD, 所以S△ACE=S△ABD,
又由(1)知△ABD∽ΔACE,
所以对应边之比等于1,
所以AB=AC,即三角形ABC为等腰三角形.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
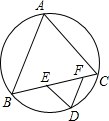 如图.在△ABC的外接圆上,弧AB、弧BC、弧CA的度数比为12:13:11.在BC上取一点D.过点D分别作AC、AB的平行线,交BC于E、F两点,则∠EDF的度数为
如图.在△ABC的外接圆上,弧AB、弧BC、弧CA的度数比为12:13:11.在BC上取一点D.过点D分别作AC、AB的平行线,交BC于E、F两点,则∠EDF的度数为 如图EF是△ABC的中位线,BD平分∠ABC交EF于点D,若AB=4,BC=6,则DF=
如图EF是△ABC的中位线,BD平分∠ABC交EF于点D,若AB=4,BC=6,则DF=
